
Abstract & Current Status
The goal of this proposal is to develop a Ground Penetrating Radar (GPR) and attach it to the flying object vehicle
called hexacopter.
Within this project we have developed a stepped frequency (SFCW) radar and pulse radar, which operates in frequency and time domains, respectively. Both radars were tested on a mine field, with attaching them to a small ground vehicle and later also hexacopter. The proposed timeline of the project was achieved and all activities within the project we’re successfully finished.
Within this project in the first year principles of GPR have been studied, generally in order to understand image interpretation and implement a GPR on a Software Defined Radio (SDR – USRP). Since the USRP device has several hardware limitations, this task represented the most challenging task. As soon as the simulations with the USRP platform provided useful information about the suitable frequency and power range, custom hardware design has followed. Developed was a frequency domain radar which uses standard telecommunications components and operates within a frequency range of 550 MHz – 2.7 GHz. The radar uses a step frequency principle and is able to generate a frequency sweep within 10 ms using 200 frequencies steps.
A time domain radar was also developed using an Ultra-Wide Band (UWB) principle. Results have shown that the radar is suitable when its used with a ground driven vehicle but performed bad when attached to the hexacopter. This is due to the inhomogeneous hexacopter movements which affect the sampling mixer on the radar front end.
Since the SFCW radar has performed better this allowed us to upgrade the existing radar to a sparse based system. This has contributed to reduce scanning time with reducing the frequency step number to only 60 % and later using compressed sensing principles to reconstruct the signal.
Within the third year software was developed to transmit data from the hexacopter platform to a PC in real-time as also store it additionally onboard.
In post-processing also Synthetic Aperture Radar (SAR) techniques has been implemented to achieve better object-to-ground contrast with satisfying results. With additional use of GPS data, the radargram could be geolocated and simplify the landmine localization. This part is still under development.
The final software was tested with a potential end user in Macedonia at Military Academia as also great interest exists from the demining centre in Slovenia.
Radar attached to the hexacopter is fully operational and is capable of detecting landmines on affected fields above as bellow the ground surface.
Project Goals
Landmines are made of metal or plastic, and there are many existing detection techniques for landmine detection. Some techniques have disadvantage, that they cannot detect plastic landmines, but only metal ones. With a use of electromagnetic radiation (EM) and by using appropriate wavelengths signal penetrates below ground surface and reflects off items with different dielectric constant or conductivity. These properties are also valid for explosive inside the plastic housing.
This project deals with methods and strategies for land mine detection using a hexacopter. The goal is to develop a low-cost and light weight ground penetrating radar using standard radio frequency components. There exist two approaches, time domain and frequency domain approaches. The first one requires a pulse with short duration, typically few 100 ps and the other approach, which is easier to implement is to observe the amplitude and phase change between the transmitted and the received signals. Since the signatures produced in the radar images from reflections off objects usually have hyperbolic shapes, we develop methods for localization based on hyperbola detection and its vertex determination. Also, we use methods based on machine learning using deep neural networks for object detection, localization and classification.
The goal of the project was to develop a small, lightweight radar and attach it to the commercial hexacopter. This was done within the following steps over a period of 3 years:
Year 1
- Prototyping antennas and antenna design,
- Prototyping principles of GPR using Software defined radio
- Defining hardware for GPR and simulate principled of generating and receiving GPR signals
Year 2
- We designed the first GPR prototype using stepped frequency principle. The GPR is very modern, it uses FPGA to process data and sending/receiving commands.
- We designed time domain GPR
- We have used a sparse radar for recovering data with random sampled data. These principles can be used in time critical applications.
Year 3
- Hardware platforms was upgraded to the version 2, with some enhancement in performances
- Data processing chain and data representation was developed
- Software for landmine detection was developed using simulated GPR data and some experimental data has been processed.
- Intensive testing was done using landmines
We have published and presented several conference papers and made demonstrations to the companies.
Summary of Accomplishments
Within this project radar attached to the hexacopter was developed. The radar and hexacopter are shown in Fig. below

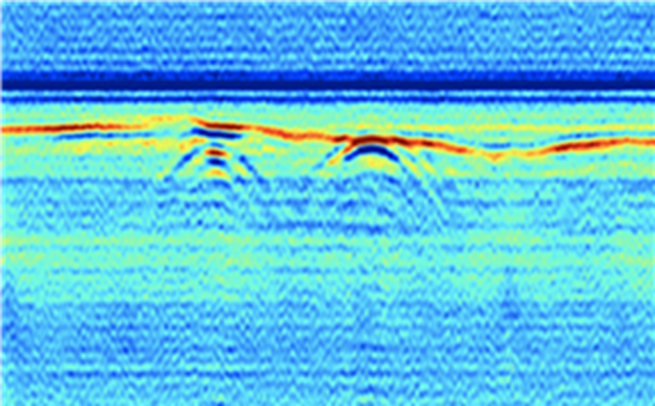
Fig. 1. (left): Antennas and small GPR attached to the hexacopter. (Right): Detected buried object detected using stepped frequency radar.
The goal of the project was to develop or use:
- Ultra Wide Band (UWB) antennas
- Design stepped frequency radar
- Represent GPR data and detect landmines.
Accomplishments
Overview of radar principles that were developed at University of Maribor, Slovenia
The first part of this section presents two methods for landmine detection. The first one uses properties of the frequency domain and describes the implementation of a Stepped Frequency Continuous Wave (SFCW) Radar, while the second method describes the implementation of an impulse radar within time domain, presenting the designs of the transmitter and the receiver. The second part of this section describes the software defined radio (SDR) implementation of the SFCW Radar, the compressive sampling version of that radar, and the signal processing approaches to automatic landmine detection.
Stepped Frequency Continuous Wave (SFCW) Radar
Stepped Frequency Continuous Wave (SFCW) Radar is a system which transmits electromagnetic radiation by increasing the frequency over a chosen band with fixed steps. SFCW Radar systems are based either on the homodyne or super-heterodyne architecture. The homodyne architecture is simpler, with only a single frequency down conversion, while the super-heterodyne performs two frequency down conversions to produce the base-band signal. The super-heterodyne architecture gives better performance. Here we first focus on the homodyne architecture and then we present implementation of the super-heterodyne structure.
Landmine detection represents a globally challenging task, because of the material they are made of and their small sizes. Land mines are made of metal or plastic, and there are many known detection principles or methods, which also include the use of animals e.g. rats. Many of them have the disadvantage, that they cannot detect plastic landmines, but only metal. With the use of electromagnetic (EM) radiation – microwaves this is not the case, because by selecting suitable wavelengths, the signal can penetrate through the ground surface and reflect off items with dielectric constant or conductivity different from those of the ground soil. This also includes the explosive which is inside the plastic land mines. This method for analysing objects below ground surface is used for decades and is known as Ground Penetrating Radar (GPR). However, commercial solutions of GPR Radars are large and require contact with the ground surface. Using experimental results with Vector Network Analyzer (VNA) the Radar parameters can be estimated and then used for implementation on small sized Printed Circuit Board (PCB), with the use of standard integrated circuits (IC). The purpose of reducing the Radar size and non-ground coupled measuring gives us the possibility of mounting the system on a small Unmanned Aircraft System (sUAS), which could be remotely controlled from a safe distance and without a direct contact with the investigated surface. Namely, many people are hurt during the land mine detection process, while this solution could avoid this.
There are many kinds of landmines present, but broadly we can divide them into anti-personnel (AP) landmines and anti-tank (AT) land mines. They differ in size and in amount of explosive inside. Because of their size the AP land mines are more challenging to detect than the AT land mines. Therefore, in this section, the focus is mainly on detecting AP landmines. As mentioned, commercial GPR Radars are well known and are based either on the time-domain or the frequency domain architecture. Within the time domain architecture-based radar, the best known is the impulse radar. The basic working principle is very straight forward, where the time delay between transmitted and received pulse, which is directly proportional to the target distance, is measured. However, it has many disadvantages that could affect our suggested system. For suitable resolution and penetration depth the impulse radar must generate pulses of width less than 1 ns and amplitudes of few volts or more. The receiving part of this kind of radar has to use an ADC with sample rate of at least few Giga Samples per second for achieving suitable resolution. Therefore, additional hardware is needed to collect the large amount of data, that makes the whole design complex, large and more expensive. Frequency domain radars don’t need high speed analogue to digital converters because the signal is down converted to lower Intermediate Frequency (IF), which makes IC design simpler and smaller in size. Therefore, this work proposes the Stepped Frequency Continuous Wave (SFCW) radar which is a subcategory of the category of frequency domain radars.
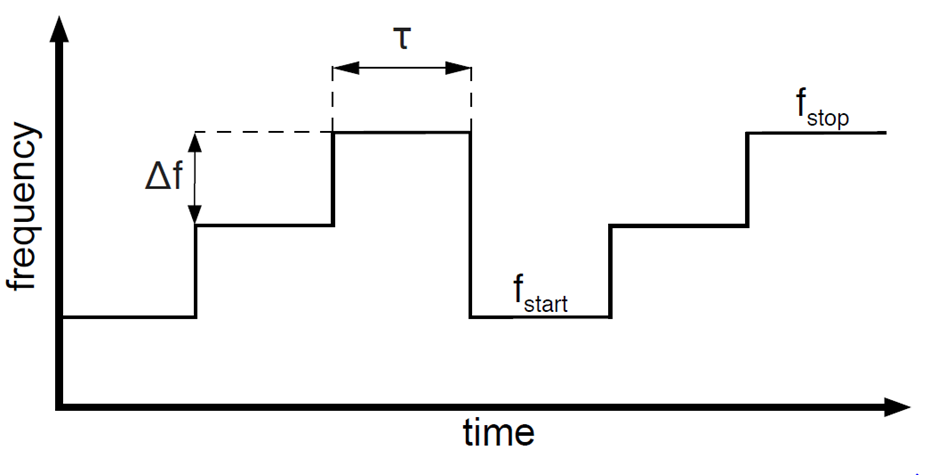
Fig. 1a. Basic working principle of SFCW Radar
SFCW Radar is a system which transmits electromagnetic radiation with increasing frequency over a chosen band with fixed steps as is shown in Fig. 1a. The frequency at given step n is switched after time and can be expressed as
fn= f0+ n∆f , n = 0,1,2,…,N-1(1)
where f0 is the starting frequency, ∆f is the frequency step size, N is the number of steps in one measurement and limits the step number between 0 and N-1. Time represents one burst and repeats continuously. The SFCW Radar bandwidth is defined as
B = N∆f (2)
and the range resolution is inversely proportional to B, where c is the speed of light. The maximum Radar range is given by , which means that at fixed B, N must be increased to increase the maximum range.
SFCW Radar systems are based either on the homodyne or super-heterodyne architecture. The homodyne architecture is simpler, with a single down conversion, while the super-heterodyne performs two down conversations to produce the baseband signal. The super-heterodyne architecture gives better performance, but homodyne architecture is usually integrated within the Vector Network Analysers (VNA). Fig. 2 shows the basic block diagram of the VNA.
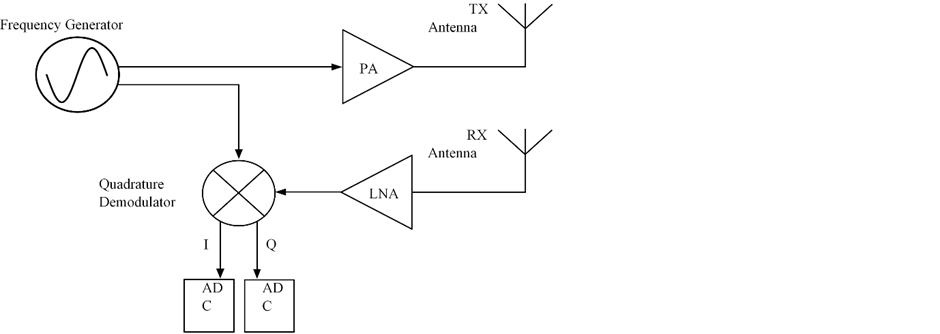
Fig. 2. Basic working principle of VNA.
Frequency hopping is performed in the frequency generator block, which has two outputs. The signal from the first output is amplified through a Power Amplifier (PA) and transmitted through TX antenna. If a target is present the signal will be back-scattered and collected by the RX antenna, where the signal is then amplified through a Low noise Amplifier (LNA). The output of the LNA is mixed in a Quadrature Mixer with the second output of the RF generator. These two signals are equal in frequency but, the received signal has a different amplitude and phase shift, because of the time it has travelled to the target and back. This result we get also from the Quadrature Mixer, where from In-phase (I) and Quadrature (Q) signals magnitude and phase are obtained. To determine the target distance, for each transmitted frequency, the quadrature signal must be collected, and is called range bin. The collected bins of magnitude and phase are now represented in the frequency domain with discrete steps. To obtain the target distance Inverse Discrete Fourier Transform (IDFT) must be performed to transform the data into time domain. For the described measurement method, it was considered that an A-scan is obtained, and the Radar is static. However, this is not useful for practical use where a GPR image is created of a B-Scan. Here the SFCW Radar has a disadvantage, compared to the Pulse Radar because it must be at the same location during the burst duration interval which lasts . Also, some more conditions must be considered, that can cause aliasing of the target. The pulse width and frequency step must be related as also the pulse repetition interval has to be several times longer than the pulse width.
EM radiation with lower frequencies can reach higher distances and penetrate deeper into medium. For GPR Radars the value of f0 is usually between 100 MHz – 500 MHz, but at the same time the bandwidth B should be large enough to achieve good range resolution. Different scenarios were simulated to prove this concept. The goal was to use parameters, which could be also used in real measurements and depend on hardware limitations which are caused mostly from the antenna and amplifier bandwidth. The simulation scenario has included two close targets, the number of steps does not exceed N = 100, and the frequency has been changed in the range 400 MHz – 3 GHz, where the bandwidth was not lower than 1.5 GHz. The purpose to keep N low is because the maximal unambiguous range should be only few meters, keeping the measurement time low. A sine wave signal was generated with fixed steps. Next the original signal was delayed for two targets which differ in range by . The purpose of simulating two targets close to each other is to determine the minimal bandwidth that enables that they can still be separated. In real scenario this would represent a land mine which is very close to the ground surface. The delayed signal was then multiplied with the original signal to implement quadrature demodulation.
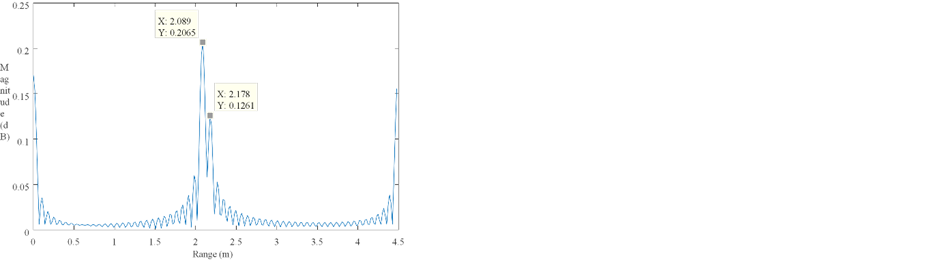
Fig. 3. Simulated SFCW Radar range profile of two targets separated by 5 cm
To generate the spatial domain signal for the range profile, IDFT is performed. Figure 3 was obtained using the following parameters: fstart=700 MHz, B=2GHz, N=60 and signal was zero-padded with Npadd=254, before IDFT was performed to obtain a longer resulting vector and get smoother range plot. The simulation result shows that the two objects can be separated even if they are very close to each other.
The simulations of a SFCW Radar gave us rough information about the parameters and limitations which should be considered. The most critical hardware part is the bandwidth of antenna and amplifier. It is challenging to design an antenna which has a bandwidth > 2 GHz and the lower frequency limit lower than 500 MHz. Amplifiers that have to be used on the transmitting and receiving side must be chosen carefully, because they are also limited with the bandwidth at lower frequencies. The switchable frequency generator can be realized using different multifunctional RF equipment. It is possible to use Software Defined Radios (SDR) as described in [1]-[2], or a VNA whose basic functionality equals the SFCW method [3]-[4]. A VNA can usually perform faster frequency switching and has also wider bandwidth, therefore we have chosen to use the Agilent E5063A ENA VNA as a frequency generator. This equipment can sweep from 100 kHz up to 6.5 GHZ, with maximum of 200 steps and output power of 0 dBm. The output power of VNA is not enough to penetrate through the ground soil, therefore, we use Mini-Circuits ZHL-4240W+ PA, with operating frequency from 10 MHz up to 4.2 GHz with 39 dB of gain. This PA has appropriate bandwidth suitable for a GPR system, with output power up to 37 dBm. The signal is then transmitted over a custom built UWB horn antenna [5], shown in Fig. 4 (left). The proposed SFCW Radar system should be Air-coupled, meaning that the antenna impedance should be well matched with the air impedance. The Radar system impedance is matched to 50 Ω, while the impedance of air Zois
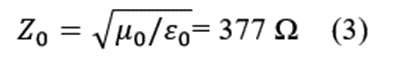
Because there is a great difference in the impedance, the antenna must be carefully designed to transmit the EM radiation through the whole frequency band with as low backscattering as possible. The relevant parameters are described as the scattering parameters or S-parameters, where the S11 parameters are most important for the antenna. The simulation is shown in Fig. 4 (right). The antenna is suitable for the specific frequency band if the Magnitude value is below -10 dB. This confirms that the built antenna can be used in the frequency range from 700 MHz up to 6 GHz. One critical point occurs at 1.3 GHz, but this should not affect the performance drastically.
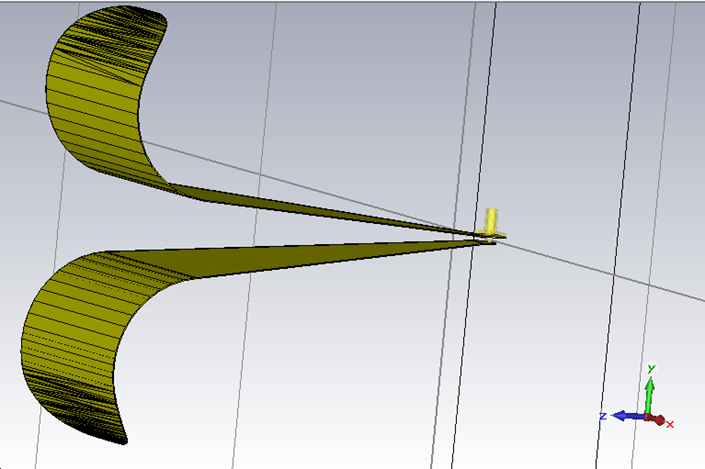
Fig. 4. (Left) UWB horn antenna [5] and (right) the magnitude of scattering parameter S11 versus frequency graph. The antenna height was 20 cm.
Transmitting and receiving antennas were the same. The signal travels different materials, which have different dielectric constants. This means that the signal is highly attenuated and needs to be amplified before the demodulation. Mini-Circuits Gali-55+ amplifier which operates in the range from DC – 4 GHz with gain of around 20 dB, was used for that purpose. The signal is then down converted in the quadrature demodulator. The output is sampled with a dual ADC to obtain the phase and magnitude. Data are further processed in Matlab Software, where also the B-Scan GPR image is created.
Experimental results using homodyne realization of GPR with VNA
To obtain experimental results, an AP land mine was buried into a polygon of size 3 m x 2 m x 1.5m, filled with mixed soil. The mixed soil contained rocks, and the rock diameter did not exceed 1 cm. The AP land mine size was 5 x 5 cm and it was buried at a fixed position, 40 cm from the polygon edge and 25 cm deep. Several B-scans were performed, where the antenna distance from the ground was varied between 5 cm and 1 m. As expected, best result was achieved with lower distances. The maximum antenna height, where the target was still recognizable was 20 cm, with more details about the parameters shown in Table II. Fig. 5 shows the processed GPR image where strong reflected signals are of darker colour. The references are marked with lines, where cross-section of blue lines indicates the actual land mine position and the green line indicates the ground surface. The results show that the surface and the land mine are clearly recognizable. The backscattered signal from the AP land mine is already present before the antenna is above it. This is because the antenna has a wide radiation pattern. This could be resolved with use of additional focusing algorithms.
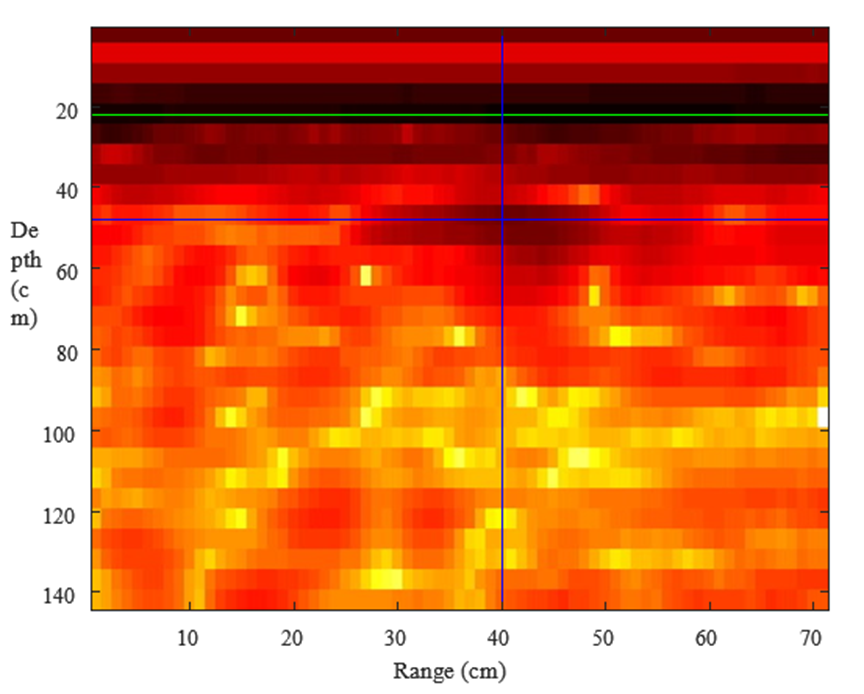
Fig. 5. GPR image obtained from measurement, where cross section of blue lines represents the buried AP land mine, and green line indicates the ground surface
The simulation and implementation of a SFCW Radar have been presented. The results have shown that an air-coupled GPR system can be implemented with use of a VNA. However, hardware parameters must be chosen carefully. It was proven that with specific parameters a buried AP land mine can be detected. The penetration depth is mostly affected by the frequency range and output power of the Radar system. The experimental results have shown that the maximum antenna height could be 20 cm for our system, to successfully detect a land mine. This could be improved with choosing a PA with higher gain, with the consideration that this would make the Radar system heavier and has a negative impact on the size and weight.
Hardware design of transmitter and receiver using a super heterodyne structure
We have designed a new platform for CW radar, which was based on homodyne architecture to reduce target aliasing and quadrature noise. We have used a low noise level amplifier used at the receiver side, which has a consequence of SNR improvement with use of external ADC. Additionally, the FPGA was used for digital quadrature mixing and on-board signal filtering. The results were stored and transferred to on-board SD card or external host computer. Fig. 6 (a) depicts the homodyne structure of the radar and Fig. 6 (b) depicts the super heterodyne structure of the radar. They differ in the receiver part, since different up and down conversion frequency are used for all generated signals. This structure was implemented, and details are depicted in Fig. 7. The realization of the hardware is shown in Fig. 8.
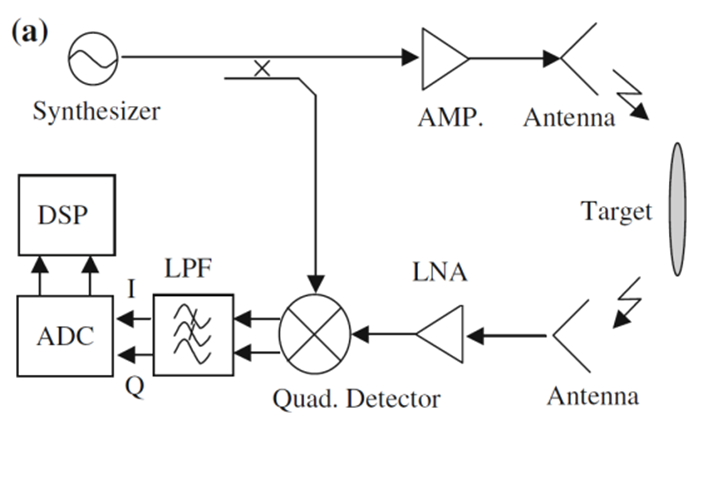
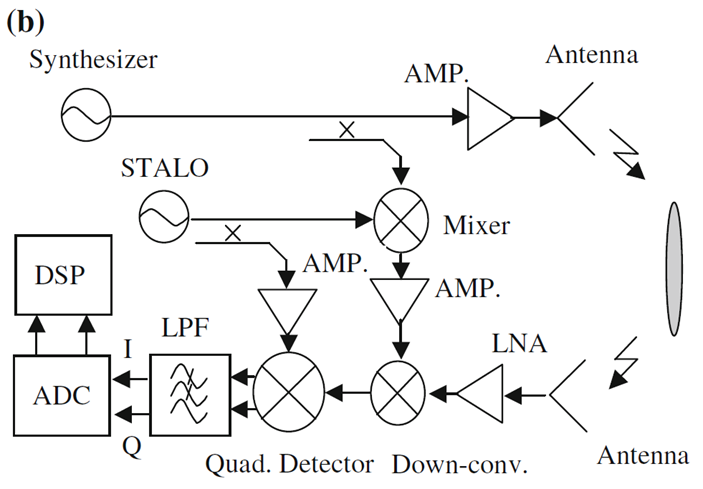
Fig. 6. A block diagram of the (a) homodyne and (b) super heterodyne stepped frequency radar.
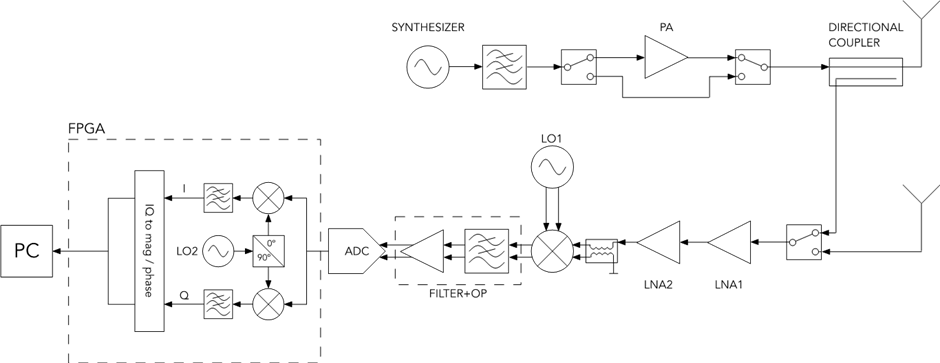
Fig. 7. Super heterodyne structure of SFCW radar.

Fig. 8. Realization of the hardware.
Calibration
The designed radar was calibrated using 4 subsequent measurements. The radar responses were captured, and the response was normalized using those measurements. Fig. 9 shows the calibration results using 1 m long wire, which was connected between the TX output and RX input of the radar. In Fig. 9 (middle and right) the averages of amplitudes and phases of the received signals and the standard deviation of 4 subsequent measurements are shown. They confirm that the phase and amplitude are stable.
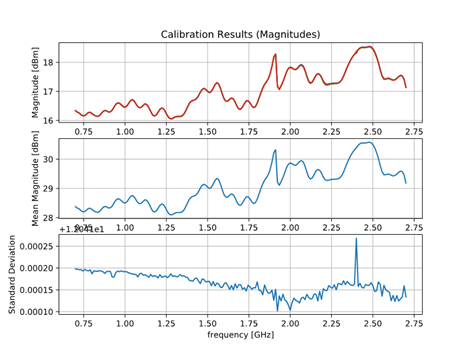
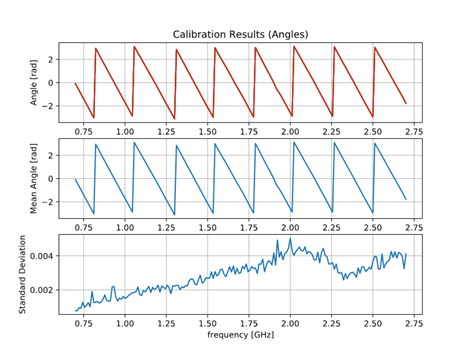
Fig. 9. Calibration. (left) Transmitted and received signals obtained with the connected TX and RX with 1 m long cable. (middle) Free space magnitude response of the radar and the standard deviation of 4 subsequent measurements. (right) phase and standard deviation of 4 subsequent measurements.
Experimental results
The radar was tested in laboratory environment. The same laboratory environment was used as in the previous example: land mine was buried into a polygon of size 3 m x 2 m x 1.5m, and the AP land mine was buried 25 cm below surface. The radar platform was moved continuously over the polygon. Figs. 10 and 11 show landmines and responses of received signals using B scan. Figs. 10 and 11 (right) show a radargram, where the figures without landmine, with landmine and with background removal are shown. The experimental results clearly show that the landmine can be detected.

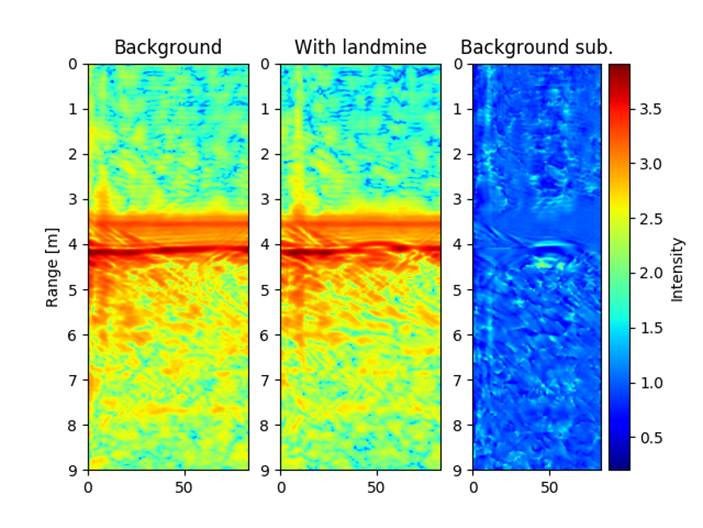
Fig. 10. B-scan of AT landmine above ground surface, landmine diameter is 27 cm and height is13 cm.

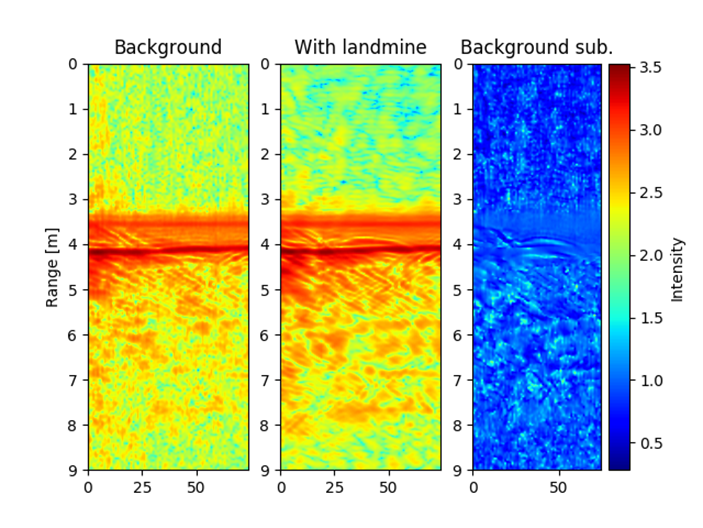
Fig. 11. B-scan of AP landmine above ground surface, landmine diameter is 7 cm and height is17 cm
Time domain radar
The Ultra-Wide Band (UWB) radar is based on picosecond pulse generator. Ultra-short pulses can be achieved with step-recovery diodes (SRD). In ON state the SRD diode behaves as ordinary signal diode. Positive signal if passes through the diode in forward regime. When signal changes polarity from positive to negative, ordinary diode switches off. SRD stores charge in forward regime and when signal changes polarity, the SRD does not switch off immediately due to stored charge. Near the end of the storage phase, PN junction increases the resistance and finally switches off the junction during the decay time, which is extremely short. Switch off phase is of the order of picoseconds for an SRD. Fig. 12 shows SRD in storage, decay and off regime when a step excitation signal is applied [9].
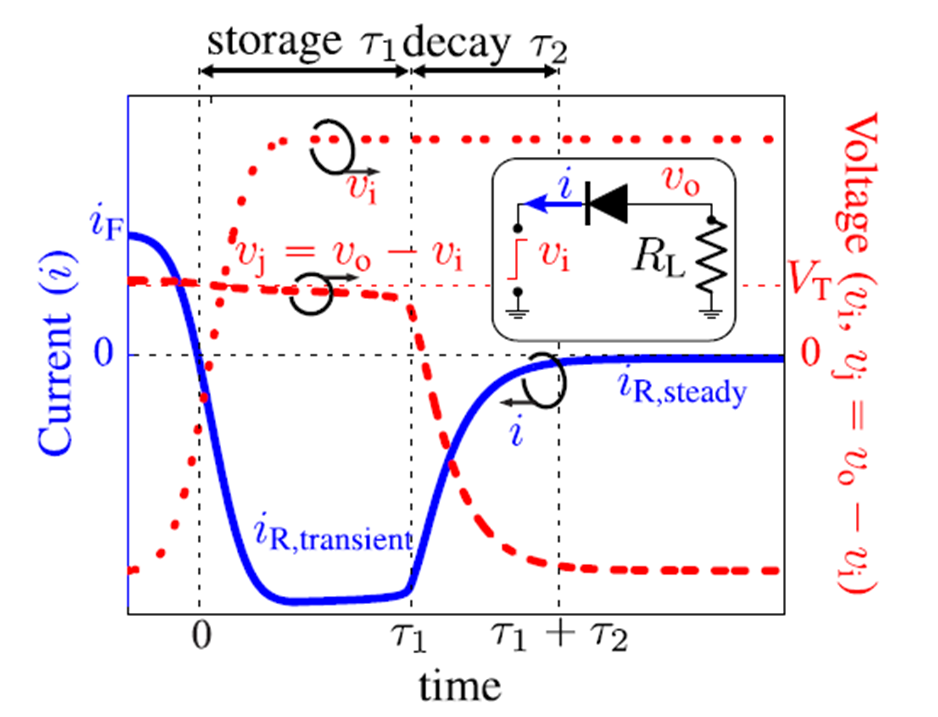
Fig. 12 Forward current iF (blue solid curve) and junction voltage vj (red dashed curve) in response to a step voltage vi (red dotted curve) from the forward to the reverse regimes.
Many designs of pulse generator using SRD have been reported in literature. Most common design is using single step recovery diode to generate a pulse with picosecond rising edge, which destructively interferes with an opposite-polarity delayed replica of it produced by a short-circuited stub. Pulse width is equal to the round-trip time along the stub. The stub configuration suffers from spurious reflections, which produces ringing tails in the output signal. We designed pulse generator based on reference [9]. The authors of [9] used two SRD diodes, one input Schottky diode for blocking input negative voltages and one output Schottky diode for pulse shaping. Generator is biased with negative DC voltage. Generator is driven by square-wave from 0-2.5 V.
We modified the described design by removing the input diode and by removing the negative DC voltage supply. We used a square-wave input from -1 V to +1 V generated by low jitter clock CDCM6208 from Texas Instruments. The used step recovery diodes are 2D528 with 50 ps decay time and 0.8 pF capacitance. For pulse shaping at output the Schottky diode 1SS351-TB-E is used as shown in Fig. 13. PCB is implemented on Rogers, R04350B laminate with εr=3.66 (Fig. 14). Pulse width and amplitude can be adjusted with R2. We used R2=6.8 kOhm and achieved pulse width of 116 ps which occupies 9 GHz of bandwidth. Fig. 15 shows the magnitude and duration of pulse.
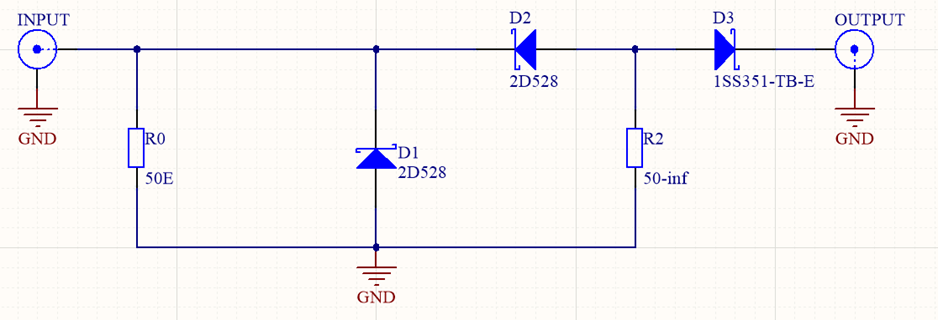
Fig. 13: Schematic of pulse generator: D1 and D2 are SRD for generating short pulse; D3 is Schottky diode for pulse shaping. R0 is input matching resistor and R2 is resistor for setting pulse width.

Fig. 14: Fabricated pulse generator
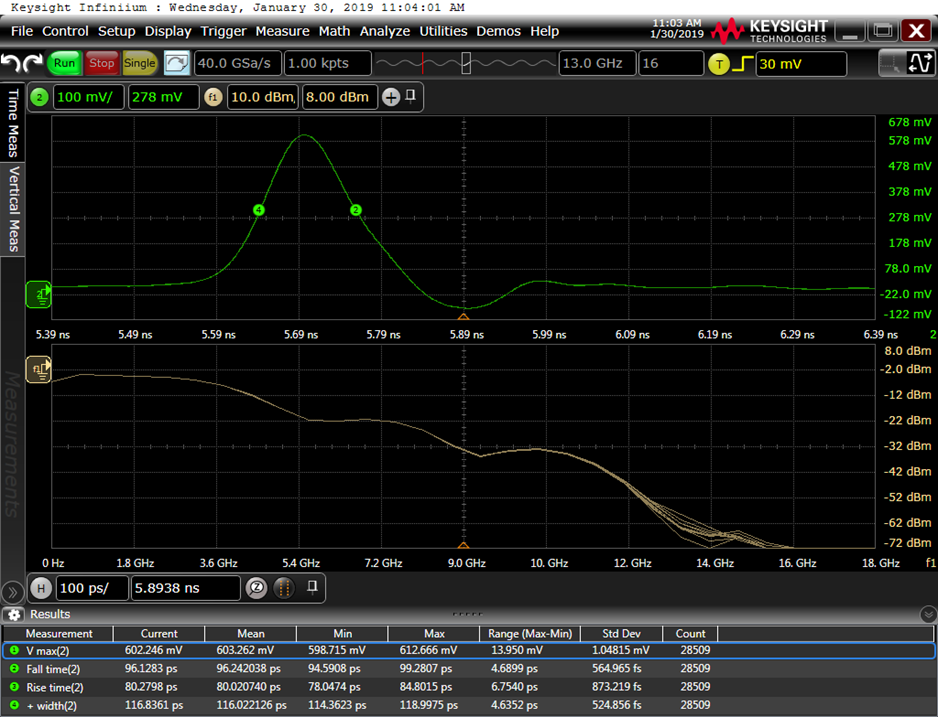
Fig. 15. Output pulse from generator captured by oscilloscope.
Sampling mixer for short pulses
To detect very short pulses in the range of hundred picosecond (about 5 GHz bandwidth), analog to digital converter (ADC) with at least 10 Gsamples/s is required. ADC with such performance is very expensive and complex. As an alternative to real-time sampling, the so-called signal stretcher is used. The idea is to sample a small fragment of the input RF signal at each time. We assume that the input RF signal is equal in many repetitions. In each subsequent repetition of the RF signal, the sampler takes the next fragment. The output of the sampler is stretched signal assembled from sampled fragments. With such sampler, we can stretch the signal from picosecond range to microsecond range.
Authors in [10] designed sampler with two diodes in a bridge configuration. The diodes are opened and closed by narrow strobe pulses, which are triggered by a precise time base. A repetitive train of identical input RF pulses with frequency f0 are required. Strobe pulses are triggered with slightly offset frequency (f0±Δf). The strobe and RF signal are mixed in such way that strobe signal slowly scans across the scanned RF signal. The received signal can be reconstructed after complete scanning cycle with a total time equal to 1/Δf. If f0 is set to 10 MHz and Δf is set to 1 kHz then the extending ratio is f0/Δf=10,000. In practice, a 300 ps pulse is extended to 3 µs. This corresponds to an equivalent sampling rate of 100 Gsamples/s.
We modified the sampler from [10] in such a way that we used fabricated balun from Mini-Circuits with bandwidth of 8 GHz instead of microstrip to slot line balun. As a strobe generator we used the previously described picosecond generator. The sampler is based on a two-diode bridge configuration. We used fast Schottky mixer diodes (Infineon BAT2402) which have small capacitance and serial resistance and forward voltage of 0.23 V. The rest of the used elements (resistors and capacitors) are the same as in the original work [10]. Fig. 16 shows the schematic of the sampling mixer.
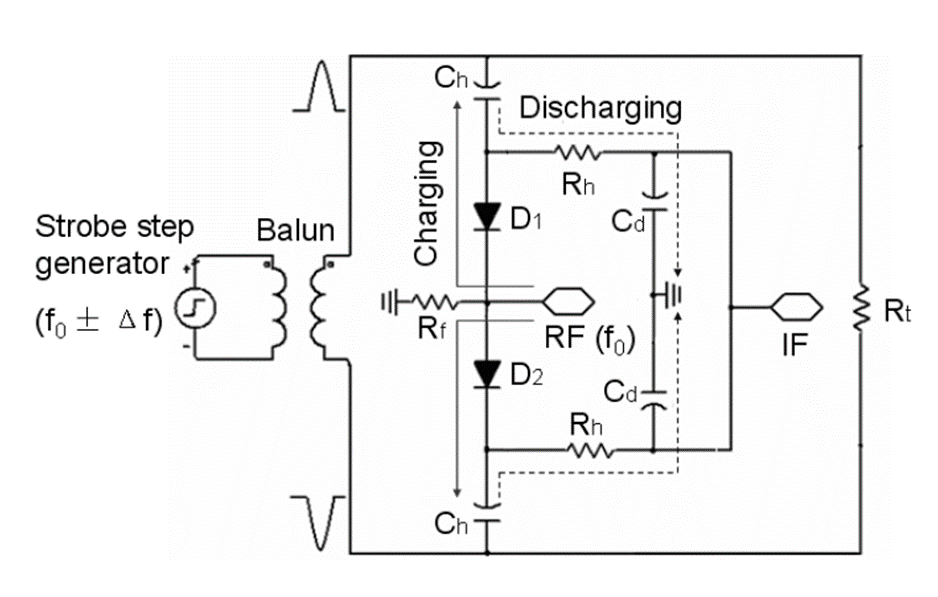
Fig.16: Schematic of sampler: pulses from balun opens the bridge and RF signal charge Ch. When bridge is closed, signal discharges trough Rh and Cd. The stretched RF signal on the IF port.
The experimental setup is shown in Fig. 17. The operational amplifier fed with f0±Δf clock is shown on the left. The strobe generator is connected with the amplifier and produces strobe pulses with repetition frequency f0±Δf at the output. The balun, which divides the input pulse into two opposite pulses, is in the middle. The opposite pulses then open the diodes on the sampler. On the right side of the figure, we can see the pulse generator fed by f0 clock and attenuator, which attenuates the sampling RF pulse. Sampler stretches the signal from the pulse generator and sends it to the IF port.

Fig.17(a): Experimental set-up of generating and sampling UWB signals.
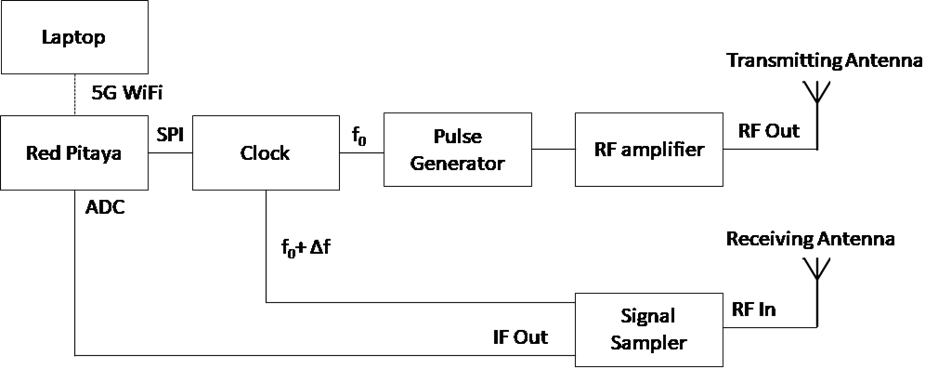
Fig.17(b): Block diagram of time domain radar.
A block scheme of the time domain radar is shown in Fig. 17(b). The microcontroller is implemented using Red Pitaya development board that is used for communication. A precision clock is used to time synchronize pulse generator and a signal sampler. The on a Red Pitaya a WiFi module and a GPS module are attached to replace a physical connection with a target computer.
Experimental results with time domain radar
The time domain radar was tested using an educational AT landmine. The land mine was buried into a laboratory polygon of size 3 m x 2 m x 1.5m, 25 cm below surface. The radar platform was moved continuously over the polygon. Figure 18 shows that the landmine can be detected efficiently using the laboratory prototype of the radar.

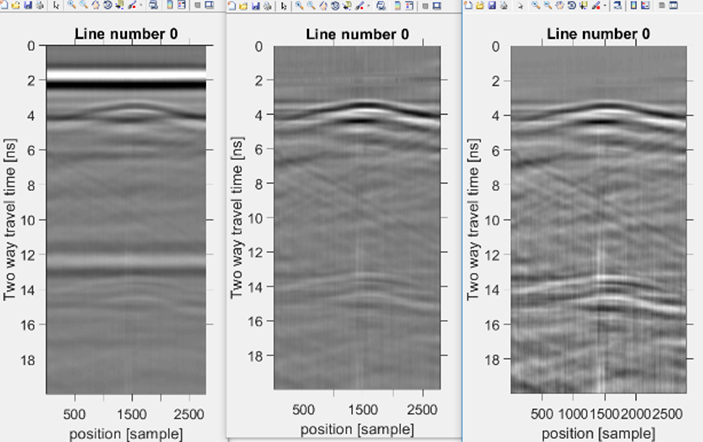
Fig. 18. B-scan of AT landmine above ground surface, landmine diameter is 27 cm and height 13 cm.
GPR Focusing
Same as in Earth observation imaging where Synthetic Aperture Radar (SAR) techniques are used, also in Ground Penetrating Radar (GPR) this algorithm can be applied. With taking advantage of the movement of a single antenna, an antenna array can be synthesized and provides high spatial resolution. To apply this algorithm the antenna parameters has to be well known as also the system setup. State of the art work is based on the Omega-K algorithm which was firstly implemented for Frequency modulated (FMCW) radar systems by [ref]. Since the FMCW dataset is similar to the SFCW, the algorithm can be accordingly modified. To obtain a focused image following main steps, has to be performed:
- Range compression
- Range Inverse Fast Fourier Transform (IFFT)
- Two Discrete Fast Fourier Transform (DFFT)
- Bulk Azimuth compression to a reference range
- Stolt Mapping
- Inverse Fast Fourier Transform (IFFT)
To proof the working principle of the Omega-K algorithm on a SFCW dataset a GPR scan has been simulated with 4 targets separated by 100 cm in depth and 100 cm in cross-range. Figure 18a shows the unfocused image, where its challenging to separate the close located targets.
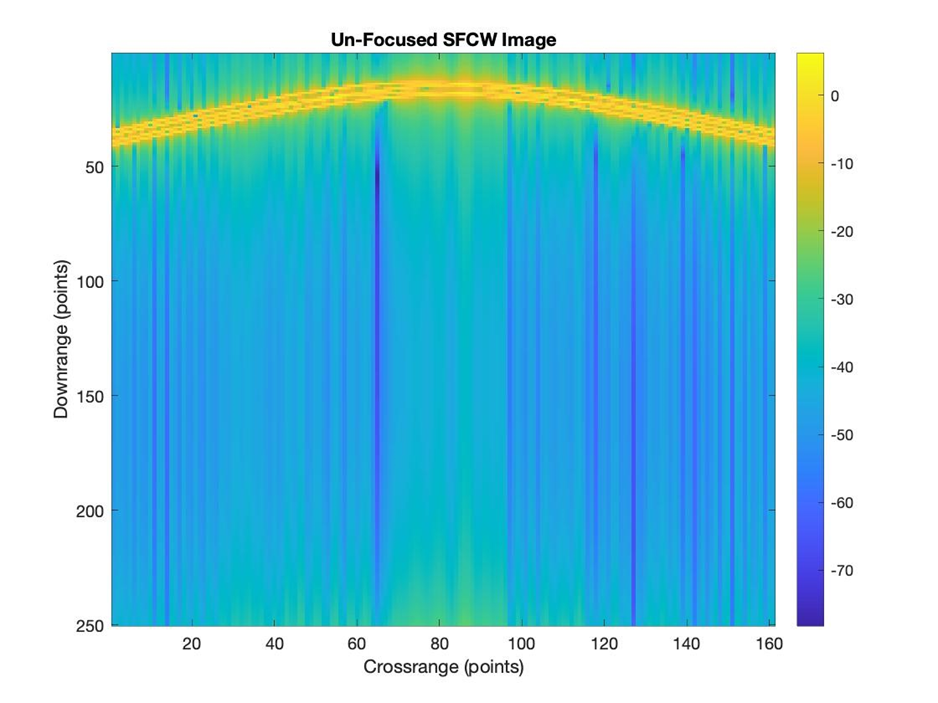
Fig. 18a Un-focused SFCW GPR image with 4 targets.
On the simulated dataset was then performed the Omega-K algorithm, where the result is visible in Figure 18b. On a detailed look we can conclude that the targets are now separated and clearly visible but have the disadvantage that a slightly location shift occurred. The algorithm was first for test purposes implemented on simulation datasets but with some additional investigations also real datasets could be focused.
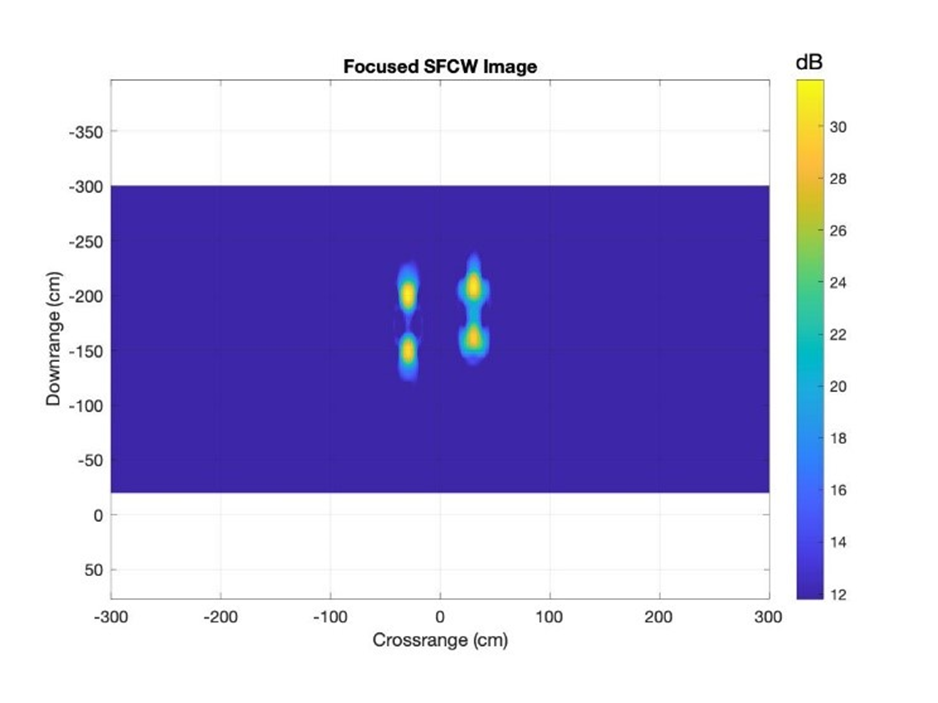
Figure 18b Close-up of focused SFCW GPR image with 4 targets after performing omega-K algorithm.
General overview of the work done at University Ss Cyril and Methodius in Skopje
At University Ss Cyril and Methodius (UKIM) in Skopje, we have focused mainly on two activities, first, the development of a Software Defined Ground Penetrating Radar (GPR), i.e. GPR implemented on a Software Defined Radio (SDR) and its Compressive Sampling version, and second, on the signal processing of the obtained GPR images (B-scans) in order to perform target detection and localization, and, additionally, target classification.
In [12] we presented a practical Software Defined Radio (SDR) stepped frequency radar implementation. It is known that the radar resolution depends on the radar bandwidth. Since the targets in GPR applications can be very small, such as anti-personnel (AP) mines, we need high resolution, which translates to a large radar bandwidth. Since hardware with a wide instantaneous bandwidth is expensive, our radar implementation is based on the Stepped Frequency (SF) radar, which requires much smaller instantaneous bandwidth than the impulse radar. In SF radar, a collection of pulses with increasing frequencies at a fixed frequency step is sent and the response is measured. After down-conversion, in effect, the discrete channel frequency response obtained from the reflections off all the targets is evaluated. By taking the Inverse Discrete Fourier Transform (IDFT), the channel impulse response is obtained, where different delays correspond to the positions of different targets. These delays are transformed into range profile, by using the electromagnetic wave velocity in the respective medium (type of soil). Our approach [12] to the SF radar SDR implementation uses a combination of baseband and RF frequency hopping. The entire RF instantaneous bandwidth at a given carrier frequency is used to accommodate the upconverted baseband signal of N pulses with increasing frequencies (a burst) in that frequency band (which we call a subband). To increase the total used bandwidth M-fold, the RF frequency of the modulated signal is hopped M times, i.e. we use M different subbands. The principle is shown in Figure 19 with M=4.

Fig. 19. Our approach to implementation of SDR SF radar
For the Software Defined Radio (SDR) GPR implementation, we used the NI USRP X310 SDR platform which has a powerful Xilinx Kintex-7 FPGA, combined with a UBX-160 radio frequency (RF) daughter-board, which covers the frequency range from 10 MHz to 6 GHz and with a bandwidth of 160 MHz [13]. Using the proposed approach, we can increase the radar bandwidth up to the entire frequency range of the USRP of 6 GHz, although our SF radar starting frequency is 500 MHz or 1 GHz, due to the wideband antenna implementation requirements. To design and implement the transmitter and the receiver on the USRP we used the open software radio development environment called GNU Radio with its graphical tool for creating signal flow graphs GNU Radio Companion (GRC). We tested the implemented radar in a field experiment at the Faculty of Electrical Engineering and Information Technologies (FEEIT) for target in the air at a distance of 15 m. We used N=30 frequencies in each burst and M=4 subbands to increase the radar bandwidth and the range resolution compared to using a single subband. The only limitation is the relatively large RF frequency switching time (settling time), but the entire measurement time is much smaller than when switching all MN frequencies, since the transmission of each burst is instantaneous, i.e. does not require RF frequency hopping. The details of the implementation and range profile plots are given in [12].
Subsequently, in [14] we developed a Compressive Sampling (CS) version of the same SF radar. Namely, since the targets are sparse, radar signals are sparse in the delay – Doppler domain for moving targets, and in the delay domain for stationary targets. The GPR application assumes stationary targets, and, thus, we do not need to treat Doppler shift. Sparsity is the main signal characteristic for using CS. CS uses reduced number of measurements (represented by using a proper sensing matrix) which is possible when the signal is sparse in some domain, which does not need to be the original domain. Due to its sparsity, reconstruction of the original signal is possible, if the sensing matrix meets certain conditions. There are different reconstruction algorithms, and in [14] we used Basis Pursuit Denoising (BPDN), which is applicable in the presence of noise. It minimizes the L1 norm of the reconstructed signal vector with a constraint that provides fidelity (i.e. measurements consistency with the reconstructed signal vector) and depends on the noise variance. Our problem is to reconstruct the sparse vector of the reflection coefficients of targets at different ranges on a range grid with J points, i.e. the range profile vector. We implement the CS SF by randomly choosing a subset of L frequencies from the N frequencies in each subband in Figure 19 and measuring the frequency response at just those L frequencies to obtain the measurement vector of dimension L. The sensing matrix for each subband is a partial DFT matrix of size LxJ, i.e. consists of complex exponentials that depend on the L randomly chosen frequencies in that subband and all the possible target distances, corresponding to all J points on the range grid. Thus, we get our mathematical model for the reduced number of measurements in each subband, by also adding the noise. We use all the available measurements in all M subbands, by constructing a measurement vector of dimension ML and a tall sensing matrix of dimension MLxJ. The reconstruction of the range profile vector of size J is performed by the BPDN. We use cross validation to determine the parameter in the BPDN constraint. The details are given in [14]. The results in [14] are obtained using the same field experiment as in [13] and compare the range profile obtained using all N=30 frequencies in each subband and IDFT with range profiles obtained using CS with L=10 and L=5 randomly chosen frequencies in each subband and BPDN reconstruction of the range profile vector. The main advantage of the CS SF radar is the reduced measurement time. Despite reduced measurement time, CS results show improved resolution. Currently, we are working on obtaining GPR images with the described SDR SF radar which requires using much higher bandwidth to obtain high resolution, needed for GPR detection of land mines. We are also working on the CS GPR version, where the number of measurements can be reduced both in the frequency domain (the stepped frequency radar number of frequencies) and in the number of scans used in the cross-range direction (i.e. number of antenna positions used to obtain the GPR image).
We also developed a simulation tool to simulate the GPR radar transmitter, the electromagnetic propagation in different media and the GPR radar receiver [15]. It uses the Matlab software package and gprMax, which is an open source software that simulates electromagnetic wave propagation in different media using the Finite-Difference Time-Domain (FDTD) method [16]. We implemented the radar transmitter and receiver in Matlab. The tool provides importing the Matlab generated SF transmit signal into gprMax, simulation of the propagation in the soil using gprMax for each transmit receive antenna position, and importing the signals from gprMax receive antenna back to Matlab for demodulation and processing to obtain the B-scan. We used this tool to obtain B-scans of different objects buried in the ground, including anti-personnel (AP) and anti-tank (AT) mines for additional signal processing.
We next describe the signal processing approaches that we used. Part of our investigations included focusing the B-scans and hyperbola detection [15]. For focusing the B-scans, we used the f-k migration to obtain more accurate object localization. In [15] we showed the result of f-k migration of a B-scan of a cylinder buried in the ground obtained using our software tool. Smaller objects in the ground produce hyperbolic signatures in the B-scan, due to the longer paths that the signal travels between the transmitter and receiver (which use collocated antennas), when the object in the ground is not exactly below the transmit-receive antennas. Therefore, an object buried in the ground can be detected and localized by detecting its hyperbola signature and hyperbola vertex. For hyperbola detection we used Hough transform, which is computationally very complex procedure. To reduce the complexity of the Hough transform, and to obtain more distinct hyperbola shapes we used the Column-Connection Clustering (C3) algorithm on the binarized B-scan image [15]. C3 algorithm produces single central strings in the place of the hyperbolic shapes, which can be wide and with irregular edges. It consists of three phases: column segmentation, column-segments connection (clustering) and central string extraction. The block diagram of the procedure is shown in Figure 20. Note that prior to applying the C3 algorithm, the ground surface reflected wave is removed by using the Singular Value Decomposition (SVD) method, where several leading components of the outer product image SVD expansion, that correspond to the ground surface reflected wave, are removed.
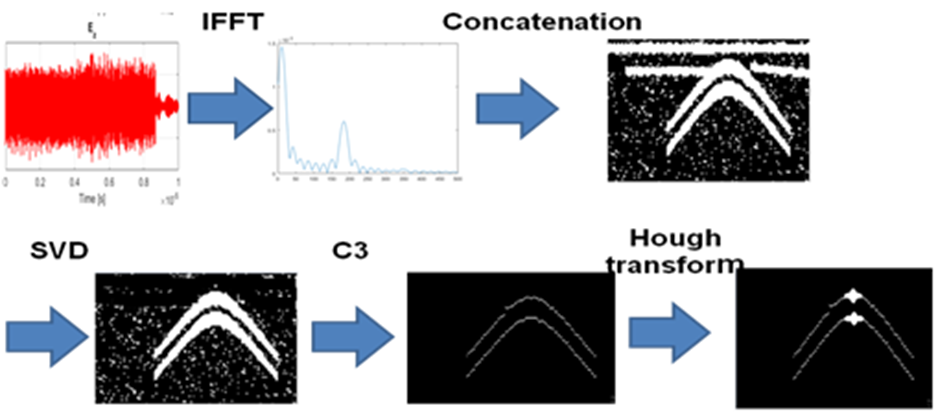
Fig. 20. The proposed signal processing procedure for GPR target detection
In [15] we presented the results of object detection and localization using the combination of C3 algorithm and Hough transform with both B-scan of a cylinder buried in the ground obtained using our simulation tool and with B-scans obtained from experimental GPR data available on the Web [17], which contain measured GPR frequency responses from different objects (such as balls, pipes, and other objects of different shapes, including land mines). The results show successful detection of hyperbolas and their vertices.
Additionally, we performed object detection, localization and classification using Faster Region Convolutional Neural Networks (R-CNN) [19]. The objects are detected and localized by the Faster R-CNN which uses Region Proposal Network to predict object bounds. Additionally, we used two classes to perform object classification, the first class being the Object class, and the second class, being the AT class, intended for recognition of AT mines. In the object class only objects with hyperbolic signatures were classified. The AT mines have distinctive signatures that are not plain hyperbolas, due to their bigger size and specific shapes they have. We trained the network with the simulated data obtained with our simulation tool and with experimental GPR data provided by other researchers (such as [17]). Additionally, we performed post processing of the Object class to distinguish between AP mines, which also give hyperbolic signatures, and other objects with hyperbolic signatures, based on the object size and location below the ground surface. The results of object detection – localization and classification are shown in [18]. We used ROC curves and confusion matrices to evaluate the detection and classification performance of our approach. Results are promising, but require further investigations and much bigger training sets, which will be provided using field measurements with our own GPR system.
Literature:
[1] V. Kafedziski and S. Pecov, “Implementation of a high resolution stepped frequency radar on a USRP,” in 2017 13th International Conference on Advanced Technologies, Systems and Services in Telecommunications (TELSIKS), Oct 2017, pp. 236–239.
[2] A. Charisma, A. Setiawan, S. A Rahayu, A. Suksmono, and A. Munir, “Matlab and gnu radio-based sfcw radar for range detection,” 08 2015.
[3] S. B. Thomas and L. P. Roy, “A comparative study on calibration technique for sfcw ground penetrating radar,” in 2017 International conference on Microelectronic Devices, Circuits and Systems (ICMDCS), Aug 2017, pp. 1–4.
[4] L. Fu, S. Liu, L. Liu, and L. Lei, “Development of an airborne ground penetrating radar system: Antenna design, laboratory experiment, and numerical simulation,” IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 7, no. 3, pp. 761–766, March 2014.
[5] A. Ahmed, Y. Zhang, D. Burns, D. Huston, and T. Xia, “Design of uwb antenna for air-coupled impulse ground-penetrating radar,” IEEE Geoscience and Remote Sensing Letters, vol. 13, no. 1, pp. 92–96, Jan 2016.
[6] N. F. A. Hakim, Chairunnisa, M. S. Arifianto, and A. Munir, “Accuracy analysis of range detection for sfcw portable through-wall radar,” in 2017 3rd International Conference on Wireless and Telematics (ICWT), July 2017, pp. 35–38.
[7] J. Burki, T. Ali, and S. Arshad, “Vector network analyzer (vna) based synthetic aperture radar (sar) imaging,” in INMIC, Dec 2013, pp. 207–212.
[8] A. Ahmed, “Design and optimization of uwb antenna for air coupled gpr applications,” Master’s thesis, The University of Vermont, USA, 10 2014, an optional note.
[9] Lianfeng Zou, Shulabh Gupta, Christophe Caloz, “A Simple Picosecond Pulse Generator Based on a Pair of Step Recovery Diodes”, IEEE MICROWAVE AND WIRELESS COMPONENTS LETTERS, vol. 27, no.:5, May, 2017
[10] Cemin Zhang, “Hardware Development of an Ultra-Wideband System for High Precision Localization Applications”, PhD diss.,University of Tennessee, 2008.
[11] S. Guo and X. Dong, “Modified Omega-K algorithm for ground-based FMCW SAR imaging,” 2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, 2016, pp. 1647-1650.
[12] V. Kafedziski, S. Pecov, “Implementation of a High Resolution Stepped Frequency Radar on a USRP”, Proceedings of 13th International Conference on Advanced Technologies, Systems and Services in Telecommunications, TELSIKS 2017, Nish, pp. 236-239.
[13] https://www.ettus.com/product/details/X310-KIT
[14] V. Kafedziski, “Implementation of a Compressive Sampling Stepped Frequency Radar on a USRP”, Proceedings of 14th Conference ETAI 2018, Struga.
[15] V. Kafedziski, S. Pecov, D. Tanevski, “Target detection in SFCW ground penetrating radar with C3 algorithm and Hough transform based on gprMax simulation and experimental data”, Proceedings of 25th International Conference on Systems, Signals and Image Processing IWSSIP 2018, Maribor.
[16] C. Warren, A. Giannopoulos, I. Giannakis, “gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar”, Computer Physics Communications, Vol. 209, pp.163-170, 2016.
[17] http://waymond-scott.ece.gatech.edu/multistaticbeamformingdata/multistaticbeamformingdata/
[18] V. Kafedziski, S. Pecov, D. Tanevski, “Detection and Classification of Land Mines from Ground Penetrating Radar Data Using Faster R-CNN”, Proceedings of 26th Telecommunications Forum TELFOR 2018, Belgrade.
Report for the period 7.11.2018-06.11.2019 for the NATO SPS 985208 project “Ground penetrating radar (GPR) Integrated to a Hexacopter for Automatic Mine Detection“ (fly-GPR) for the Partner Country Institution “Ss Cyril and Methodius University” (UKIM) in Skopje, Republic of North Macedonia
Prepared by Professor Venceslav Kafedziski, Partner Country Project Director, Faculty of Electrical Engineering and Information Technologies (FEEIT), UKIM, Skopje
The planned activities for the third year of the project at the “Ss Cyril and Methodius University” in Skopje, Republic of North Macedonia were improving the implementation of the GPR radar on a USRPSoftware Defined Radio (SDR) platform,accommodating the processing method for its use on a drone over terrain with variable elevation,developing theCompressive Sampling Stepped Frequency Ground Penetrating Radar, and improved Data Analysis using the methods of Machine learning. We performed all these activities as planned. Our work is described in four publications, that will be cited in a subsequent section on publications of this report.
Part 1. Work done at UKIM on GPR implementation on a USRPSDR platform
During the previous work on the project, we developed the implementation of the Stepped Frequency (SF) radar on a USRP. The main advantage of the SF radar is the reduced instantaneous RF bandwidth, since the bandwidth depends on the pulse duration only. It is well known that radar resolution depends reciprocally on the total bandwidth, which in turn depends on the total number of pulses with different frequencies used and the frequency step. The main drawback of the SF radar is the increased time to send all the pulses, which results in increased measurement time. On the other hand, processing can be done after collecting all the measurements, i.e. it does not have to be in real time. Since the RF circuit cannot change the frequencies instantaneously (i.e. it requires some settling time), this approach requires a long data collection time. We solved this problem by generating a baseband stepped frequency signal, and then upconverting it to RF frequency. We implemented our radar system (both the transmitter and the receiver) on a National Instruments (NI) Universal Software Radio Peripheral (USRP) device, which is a Software Defined Radio (SDR) product. The USRP uses a sampling rate of up to 200 MSamples/s and RF daughterboards with an RF bandwidth of up to 160 MHz (baseband of maximum 80 MHz), which does not give the required resolution for some applications, like, for instance, the Ground Penetrating Radar (GPR). In order to increase this bandwidth, we proposed an original approach to a SF radar. We combined two existing approaches, the first using a frequency hopping signal in the baseband, and then upconverting the signal to the RF, and, the second, using a frequency hopping of the RF frequency. On one hand, our approach dispensed with the need of using an expensive hardware with a very wide RF bandwidth that would be required by a purely baseband frequency hopping approach, and, on the other hand, our approach reduced the necessary time for frequency hopping the entire bandwidth, that would be required by a purely RF frequency hopping approach. Thus, instead of hopping each frequency, we used a frequency hopped baseband signal (a burst), and, then, we hopped the frequency of the RF carrier in different frequency bands (subbands). In this way, we could arbitrarily increase the radar bandwidth (limited only by the total frequency range of the USRP), and, thus, arbitrarily increase the radar resolution.
In our investigations we used Ettus’ X310 USRP with Xilinx Kintex-7 FPGA and UBX-160 RF daughtherboard with frequency range between 10 MHz and 6 GHz and 160 MHz bandwidth. The USRP was connected to a desktop PC via dual 10 Gigabit Ethernet card and PCI Express interface which could enable sampling rates of up to 200 MSamples/s (Full Duplex). We used GNU Radio version 3.14.1 with GRC (GNU Radio Companion) and UHD (USRP Hardware Driver) API version 3.14.0.
The work done in this project period extended the application of the radar to underground applications, i.e. we developed the GPR version of the Stepped Frequency radar. Due to the small size of the objects, such as anti-personnel mines, to increase resolution much larger bandwidth was required. Also, the random phase jumps that appear when hopping the RF frequency posed a much larger problem now, since we have short distances from the objects. Also, there could be multiple targets, so that phase linearization was not an option. We compensated the phase jumps by resending the last frequency from the previous subband as the first frequency in the current subband, identifying the phase jump between these two measurements, and compensating for the phase jump for the entire current subband. Instead of a stepped frequency radar within the instantaneous RF bandwidth (subband), we implemented an OFDM radar in each subband, i.e. at each RF frequency. The transmitted signal was generated by taking an IFFT of the frequency domain synthesized signal, which consisted of 8 frequencies within the UBX-160 RF bandwidth. The number of frequency bins was 256. In order to improve the performance by averaging, we repeated the signal 64 times. The receiver performed an FFT of the received signal, thus identifying the vector of the transfer function in each subband, Concatenating all these vectors, we were able to use a total bandwidth of up to 5 GHz. Finally, an IFFT of this large vector produced the range profile. The experiments were conducted outdoors, in the FEEIT yard, using an anti-tank (AT) mine (model VTMM-1) as the buried object, shown in Fig. 20a. The AT mine diameter is 30 cm, with height of 9 cm and weight of 8:6 kg, from which 5-6 kg is the explosive content (TNT). The object was buried approximately 10 cm below the ground surface. The survey line was 190 cm long, and the antennas were positioned 50 cm above the ground. The experiment was done using 45 subbands, each of 80 MHz bandwidth, giving a total bandwidth of 3600 MHz. Also, 26 A-scans were measured along the survey line, and the spatial step between A-scans was approximately 7 cm.
The post-processing has to deal with other issues, besides the phase-jump compensation. The crosstalk wave between the transmit and receive antennas and the surface reflected wave can have high energy, and these waves often mask the targets. This is marked as clutter. In order to reduce the effects of the clutter, we proposed to use the Singular Value Decomposition (SVD) approach, where SVD of the B-scan is performed. Since the singular values represent energy coefficients in the B-scan image expansion in terms of left and right singular vectors, we exclude the terms corresponding to the largest singular value in order to reduce the effects of the antenna crosstalk and the ground reflected wave.


Fig. 20a. GPR experiment using USRP X310 in the FEEIT yard; left – setting; right – AT mine used
As mentioned above, the phase compensation procedure should be applied on every A-scan of the B-scan, in order to obtain correct information. Fig. 20b shows the phase response at a particular antenna position, before and after the phase jump compensation. The phase response is nonlinear, which is a consequence of the presence of multiple targets (surface and AT mine). However, the abrupt changes in the phase in Fig. 20b left cause incorrect range estimation and image distortion, making the target detection impossible.
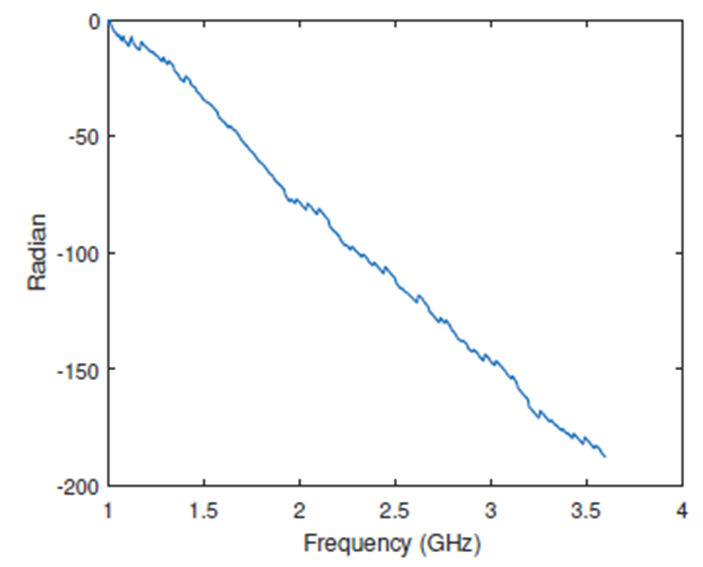
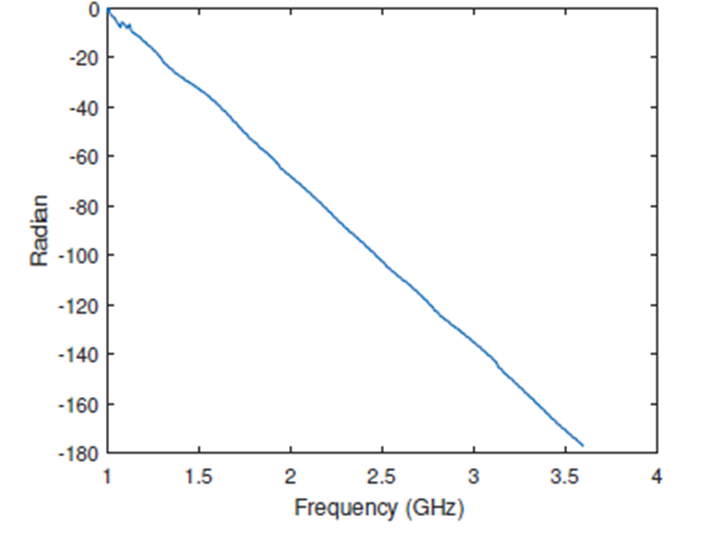
Fig. 20b. Phase response, left – before the phase jump compensation; right – after the phase jump compensation
The B-scan is shown in Fig. 20c. The target is visible, and the target location can be easily identified. The image on the left shows the B-scan with no cancellation of the crosstalk and surface reflected wave, and the image on the right shows the B-scan with the SVD method for clutter removal used.
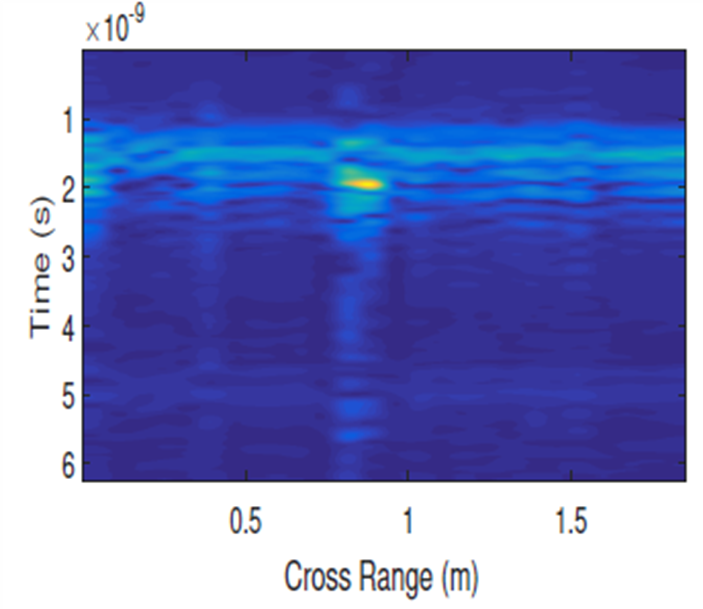
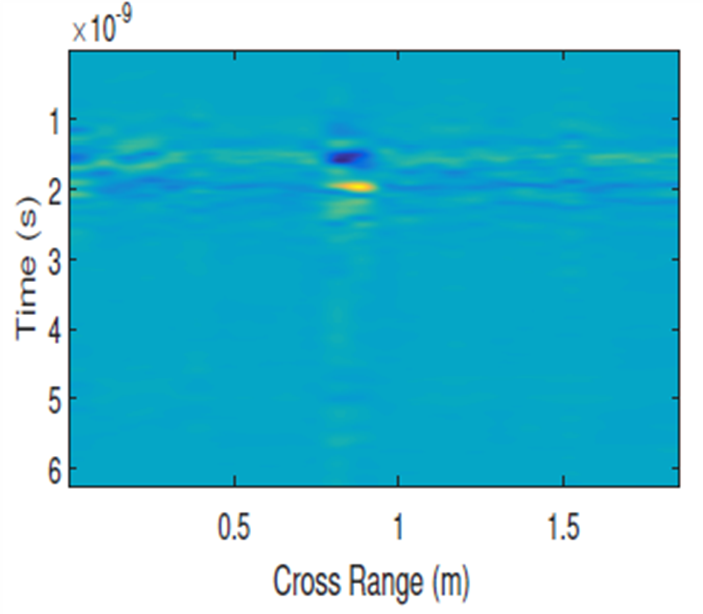
Fig. 20c. B-scan of the buried AT mine; left – with no clutter removal, right – with SVD clutter removal
Part 2. Work Done at UKIM on Compressive Sampling GPR
The work done in the previous project period included the development of random frequency radar, i.e. compressive sampling stepped frequency radar. We implemented a Compressive Sampling (CS) software defined stepped frequencyradar using a USRP SDR. The reason for this is the fact that the Stepped Frequency radar suffers from large data collection time in order to increase resolution.
Radar signals are sparse in the delay – Doppler plane, and therefore, convenient for use of Compressive sampling. We reduce the data collection time is by using compressive sampling, i.e. transmitting at randomly chosen frequencies only. Compressive Sampling (CS) provides framework for sparse signal detection and estimation. SF radar is a perfect candidate for CS, since there is sparsity in range (and Doppler) domain and a number of transmitted and received pulses with different frequencies to obtain measurements of the frequency characteristics. By randomly choosing a subset of the transmit frequencies we reduce the measurement time. In the previous project period we applied CS to the combined baseband-passband SF radar for detecting targets in the air, by either choosing random frequencies in each subband separately, or doing it throughout the entire used bandwidth.
We briefly explain the principle of CS. An underdetermined system of linear equations has more unknowns than equations and generally has an infinite number of solutions. In order to choose a solution to such a system, extra constraints or conditions must be imposed. In compressed sensing, this constraint is sparsity, allowing only solutions which have a small number of nonzero coefficients. To enforce the sparsity constraint when solving for the underdetermined system of linear equations, one can minimize the number of nonzero components of the solution, i.e. the L0 norm. For many problems it is probable that the L1 norm is equivalent to the L0 norm, in a technical sense. Besides sparsity, reconstruction fidelity has to be taken into account by adding a constraint (for measurements in the presence of noise), which gives the BPDN formulation of the optimization problem
min ||x||1 s.t. ||y-Ax||2< 0
We now describe the principle of compressive sampling stepped frequency GPR radar (random frequency radar), applied on a B-scan. Imagine we have a 2-D
measurement region of two-dimensional variable (z, x) where z ∈ [0,Ru] is the range (depth) variable, Ru = c/(2∆f) is the unambiguous range, and x ∈
[0,Rmax] is the cross-range variable (Fig. 20d). The depth coordinate z can be discretized into J points [z1, z2, . . . , zJ]T, which defines the resolution ∆z =
Ru/J. Likewise, the cross-range can be discretized into K points, [x1, x2, . . . , xK]T, defining the resolution ∆x = Rmax/K. By placing the transmit-receive
antennas at a cross-range position m∆x, where m ∈ [0,M] (we set M = K), we can calculate the corresponding delay to any point on the grid.
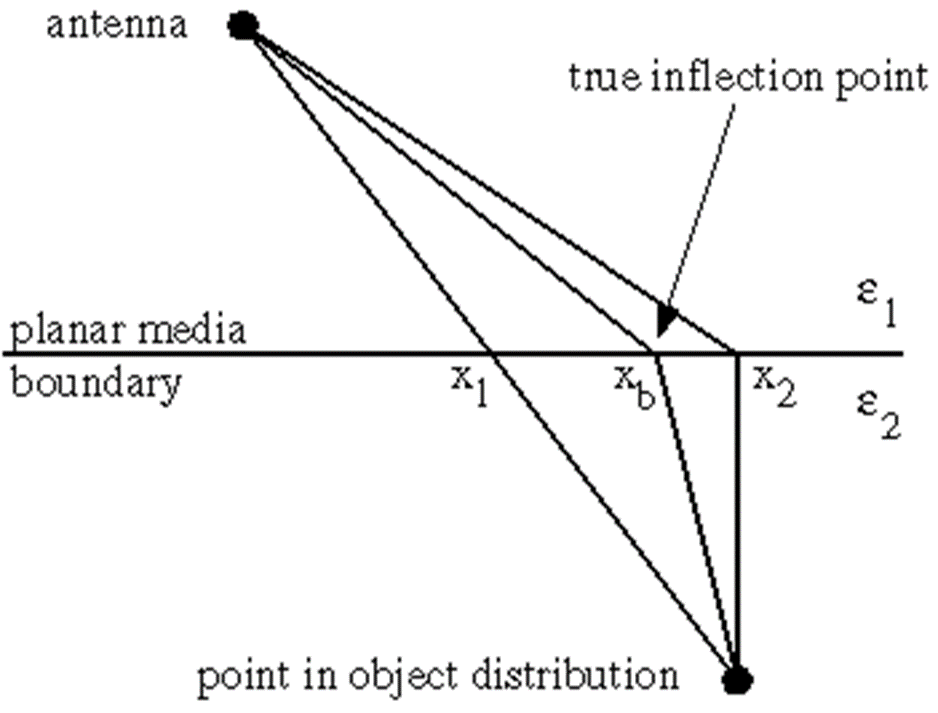
Fig. 20d. Propagation scenario for a GPR radar
Assuming point target model with a maximum number of targets equal to JK on the grid (some of them are non-existent) and isotropic antenna, the measured frequency response hm(fm) at the m-th antenna position is
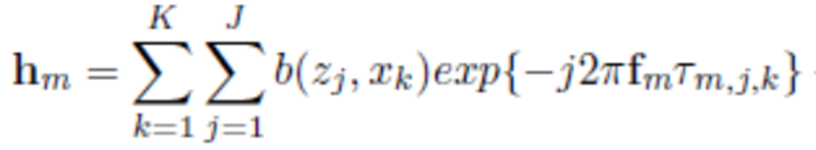
where fm is the vector of N transmitted frequencies at the m-th position, hm is the channel frequency response at these frequencies, b(zj , xk) denotes the reflection coefficient of the target at the position (zj , xk) and τm,j,k represents the roundtrip propagation delay from the radar transmit antenna to the radar receive antenna. We introduce the N×JK dictionary matrix and the sparse JK×1 vector of reflection coefficientsb, obtained by column-wise concatenation of all the b coefficients. After taking a subset of measurements, by introducing the LxN measurement matrix , constructed by randomly choosing L rows from an NxN identity matrix, we obtain
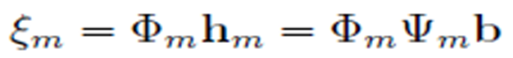
Taking Q (out of a total of M) antenna positions, introducing the two new matrices
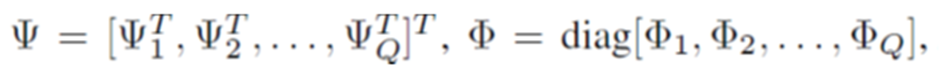
and taking the noise into account, we obtain
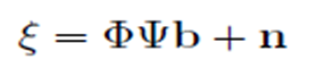
We used the Basis Pursuit Denoising (BPDN) problem formulation
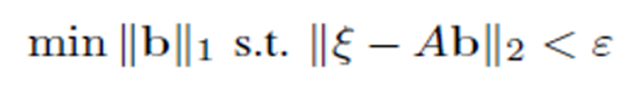
where parameter accounts for sparsity vs fidelity trade-off. The choice of the parameter is crucial for the algorithm performance and reflects the trade-off between the sparsity (fewer non-zero components of b) and the reconstruction fidelity (making close to Ab in terms of the squared error).
To improve the reconstruction results, we used structured sparsity models for the support of the nonzero values in the B-scan. Structured models are divided into two groups, deterministic and probabilistic. Deterministic structured sparsity models include group sparsity (group/block), hierarchical sparsity (trees) and graph sparsity (general sparsity patterns). Deterministic models assume prior knowledge on the geometrical structure of the sparse signals and restrict the feasible set to those signals that comply with the assumed geometrical model. Probabilistic structured sparsity models use Markov Chains (MC) for 1D signals and Markov Random Fields (MRF) for images to model the structure of the signal support. We use an adaptive model which estimates the sparse signal, its support, and noise and sparse signal parameters jointly and iteratively. Since the objects have some non-zero size in the cross-range coordinate, the scatterers are not point scatterers, but occupy certain regions. Although considering 2-D regions would result in superior performance, here we restrict to 1-D regions in the cross-range coordinate. We assume known size of the objects (for instance, we can have land mines of known size buried in the ground) and use groups of adjacent coefficients of this size for the reconstruction (Fig. 20e). We use the group BPDN, where the mixed l12 norm replaces the l1 norm, i.e. the l2 norm is used within the group, and the l1 norm is used for the vector of group norms.
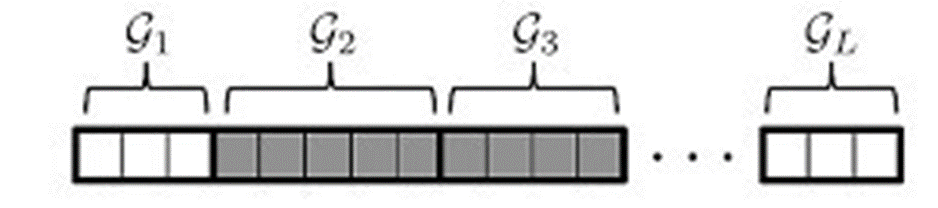
Fig. 20e. Group sparsity
In our second approach, the unknown signal coefficients are represented as the product of two random variables bn = snγn, where sn ∈ {0, 1} is an indicator of support set membership, and γn ∈ C is the amplitude of the nonzero bn, introducing the hidden random variables H = {s, γ}. We assume Bernoulli-Gaussian mixture model for the coefficients
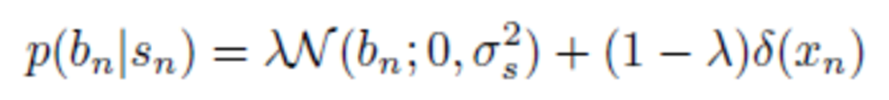
and Markov Chain Model for the sparsity support of the row-vectorized B-scan. We use the turbo-GAMP algorithm, which solves the problem of finding the coefficients, iterating between finding the coefficients and finding the support. The turbo-GAMP iterates between exploitation of the observation structure and exploitation of the pattern-structure, using the framework of Belief Propagation (BP) and its Generalized Approximate Message Passing (GAMP) implementation. Additionally, model parameters are estimated using the Expectation-Maximization (EM) algorithm, where P denotes a set of model parameters, i.e. prior means, variances, etc., which are deterministic unknowns
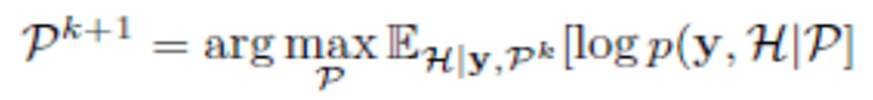
Simulation results were obtained using real data from the Web. The measurement setting is shown in Fig. 20f, where we use the data from the T1-R1 pair. The transmit and receive antennas are at h = 27.8 cm above the ground. The B-scan includes an anti-tank mine VS-1.6 of diameter 22.2 cm and height 9.2 cm (buried at 11.5 cm depth in the center of the image), two antipersonnel mines TS-50 of diameter 9 cm and height 4.5 cm, buried at a depth of 1.5 cm and set apart at 20 cm distance from the AT mine, and additional TS-50 set at 45 cm to the right of the center, buried at 2 cm depth. The AT mine and the AP mine are shown in Fig. 20g.
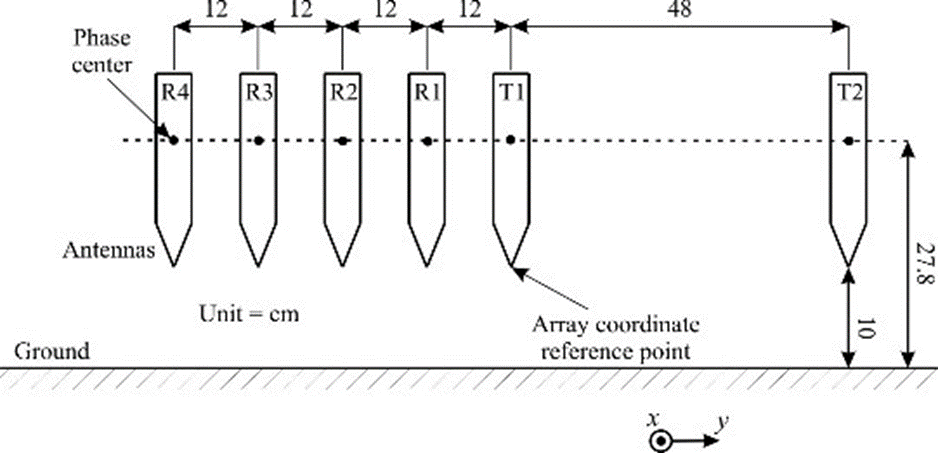
Fig. 20f. Measurement setting for the data from the Web


Fig. 20g. Left – AT mine, and right – AP mine used in the experimental data from the Web
Simulation parameters are as follows. The total number of frequencies is N = 401, out of which we randomly choose P = 100 frequencies. The total number of antenna positions is 60 at a step of 2 cm, in the range from -60 cm to 60 cm, out of which we randomly choose Q = 40 antenna positions. Thus, we use around 16% of the total number of measurements. The groups in the group sparsity approach are made of 5 elements. The value of the parameter used for simple and group reconstruction is p = 0.035. For the MC model-based results we used 10 iterations per GAMP execution and 10 turbo iterations. The results from Fig. 20h show improved object representation when using CS methods, compared to reconstruction using the IFFT method (upper left image). The model-based sparsity using the Markov Chain model (lower right image) shows the best performance of all.
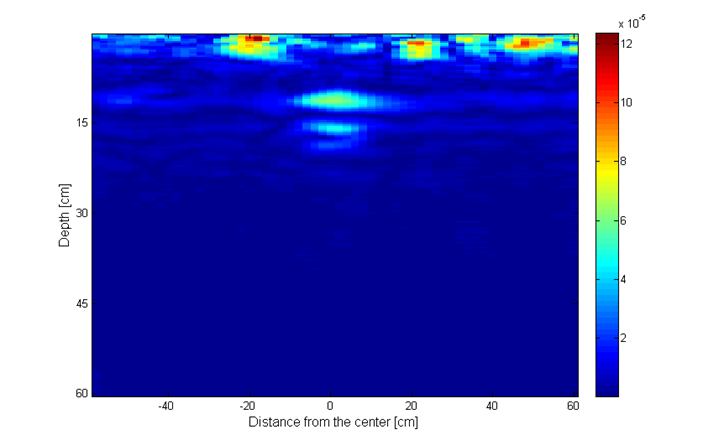
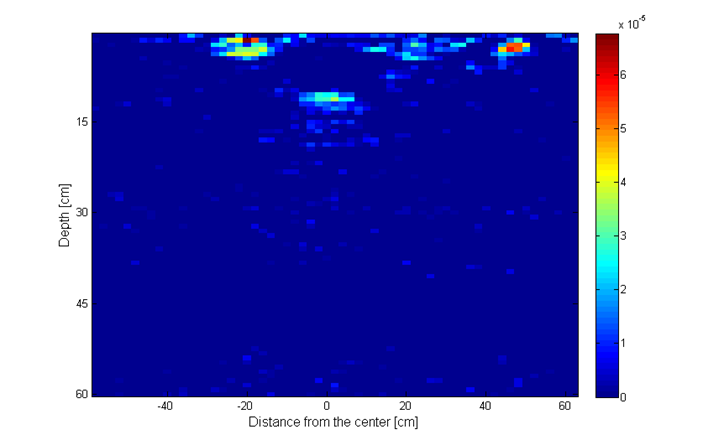
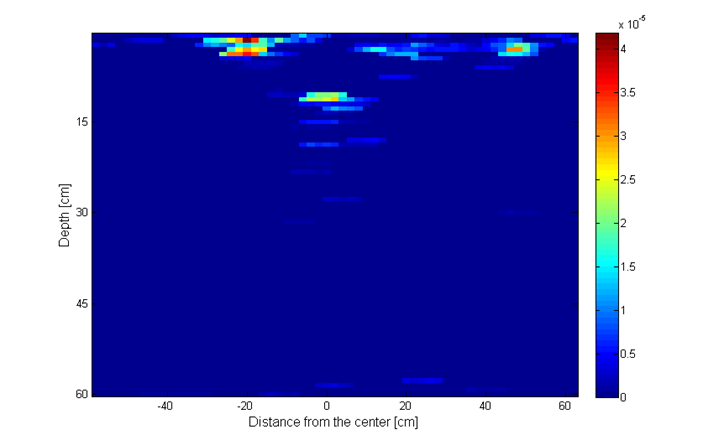
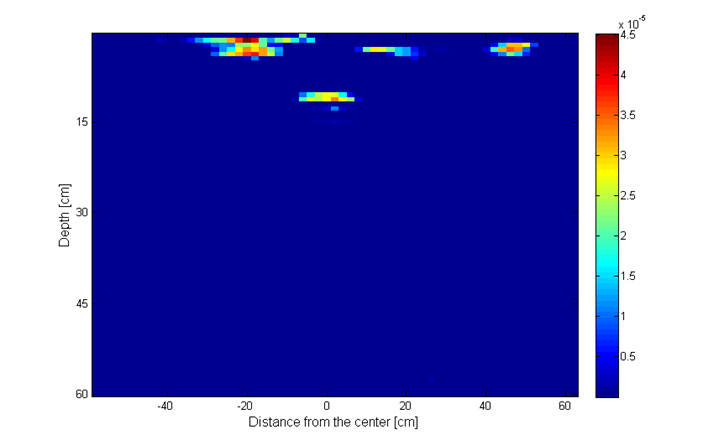
Fig. 20h. Image recosntruction using: upper left – IFFT; upper right – simple sparsity; lower left – group sparsity; lower right – MC mode.
In conclusion of this part, compressive sampling approaches reduce measurement time, increase resolution, and improve object representation. Markov Chain model-based approach shows the best performance compared to using simple sparsity and group sparsity.
Part 3. Work done at UKIM on Integration of Elevation Correction with Surface Reflected Wave Removal in UAV Mounted GPR Systems
Mounting and integrating GPR systems with drones gives a whole new range of opportunities (e.g. investigating inaccessible terrains).The main drawback of using GPR on a drone is the variable elevation of the terrain of interest. This problem is easily compensated in a conventional cart mounted GPR system.The GPR-drone integration needs a more elaborate approach. Variable elevation can potentially introduce distortion of objects in the radar image and aggravate the process of surface wave removal. The elevation correction algorithm, known in the GPR literature, on its own, is not good enough for detecting low-reflective targets or targets masked by clutter. We proposed the combination of elevation correction algorithm and the Singular Value Decomposition (SVD) based surface reflected wave removal. To prove the concept and evaluate performance, two simulation examples were created using the software package gprMax. The object recognition potential of the proposed approach was analyzed using Faster R-CNN network.
The elevation correction algorithm proposes substitution of the air layer with soil layer. Thus. is the added propagation time at each survey point, where is the propagation time in the air and is the propagation time if the air were replaced by soil, refer to Fig. 20i.
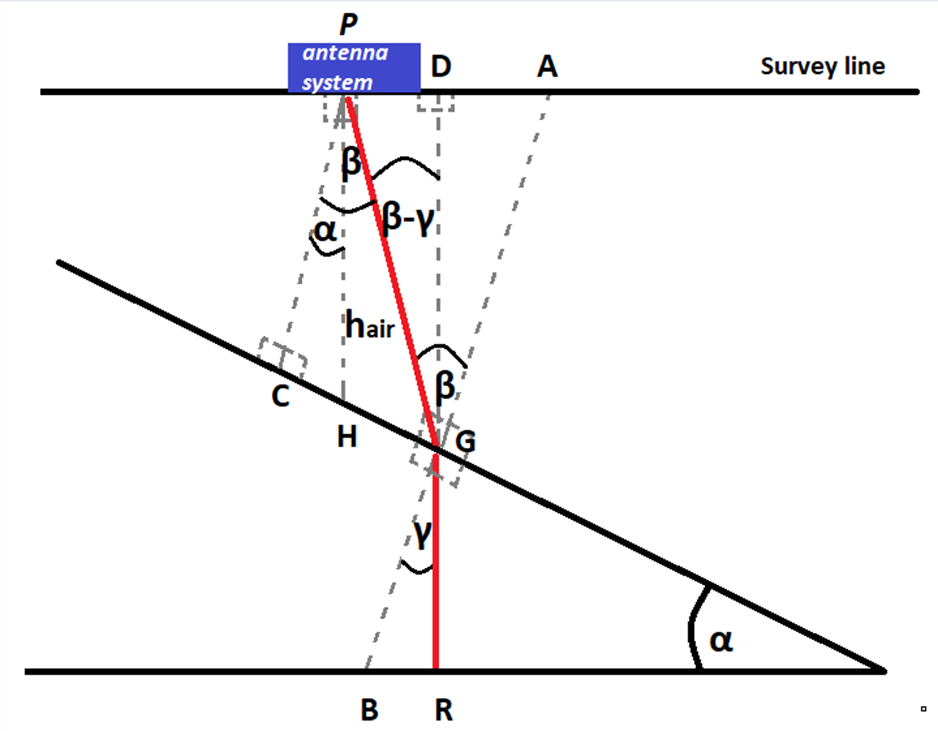
Fig.20i. Elevation correction algorithm scenario
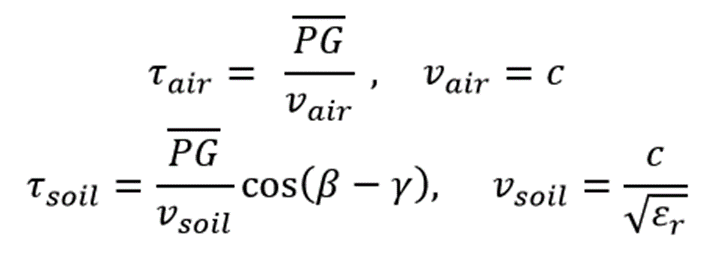
We also use the Snell’s law
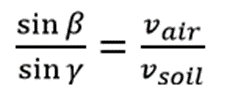
The approximation can be used when .
To simulate propagation in the ground, we used the gprMax software, which we have already used during the previous reporting periods. GprMax is an open source software that simulates electromagnetic wave propagation in different media, by solving Maxwell’s equations in 3D using the Finite-Difference Time-Domain (FDTD) method. FDTD method is based on space and time discretization (∆x, ∆y, ∆z, ∆t). We previously developed a software tool using a combination of Matlab and gprMax software packages for simulating the radar transmitter and receiver signal processing (using Matlab) and the electromagnetic propagation in the soil (using gprMax).

Fig. 20j. Block diagram of our simulation software tool
In order to obtain the radar B-scan over a sloped terrain, as shown in Fig.20j, we developed a gprMax model to simulate propagation. To obtain the B-scan we introduced antenna movement in the direction of x axis. Antennas are placed in the air, since a GPR mounted on a drone is simulated.
Model dimensions are 3.5×1.11×0.009 meters along the x (cross range), y (depth) and z axis, respectively. The discretization step is set to 0.009 m in each direction. The minimum distance from the antennas to the ground is 10 cm, the maximum distance from the ground is 90 cm and the antenna separation is 10 cm. The medium is a homogeneous soil with relative dielectric permittivity . The object is a rod made of Perfect Electrical Conductor (PEC) material, with a length of 50 cm and height of 20 cm. We used an impulse radar in the simulation.
The post-processing phase is crucial for enhancing the B-scan quality and increasing the probability of object detection. There is a lot of redundant information from the B-scan, marked as clutter (antenna coupling wave, surface reflected wave, etc.). The clutter can cause masking of targets. We use the Singular Value Decomposition (SVD) removal method for clutter reduction/removal. We perform an SVD on the B-scan. We exclude the terms corresponding to the several largest singular values, in order to reduce the effects of the ground reflected wave (usually removing a single coefficient suffices). The SVD analysis is based on orthonormal basis vectors (horizontal and vertical) and can be directly applied on the antenna crosstalk wave. However, using the SVD for the surface reflected wave removal on a sloped terrain can cause removal of other parts of the image potentially containing useful information, besides the surface reflected wave. Therefore, terrain flattening is performed prior to applying the SVD method on the ground reflected wave. In Figs. 20 l-20 m we show the B-scans after applying different phases of the proposed approach. We notice that the final image shows the object in the right position, while the clutter is entirely removed (from both the antenna crosstalk and the surface reflected wave effect).
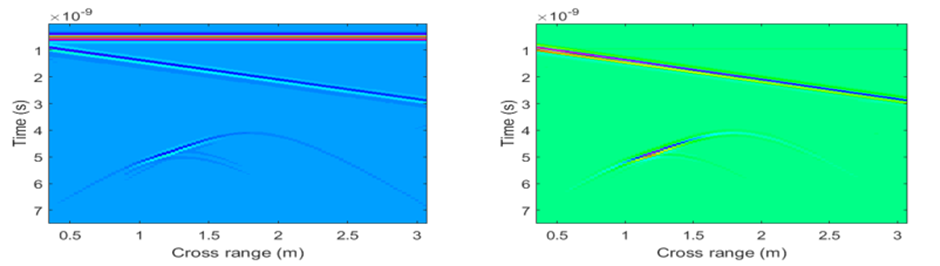
Fig. 20k. Left – Original image; right – After antenna crosstalk removal using SVD
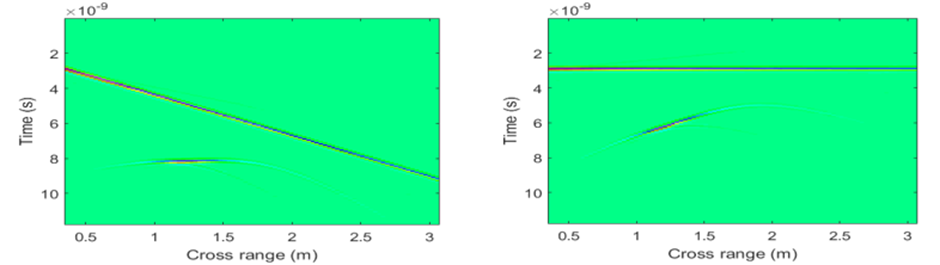
Fig. 20l. Left – After the elevation correction; right – After the terrain flattening
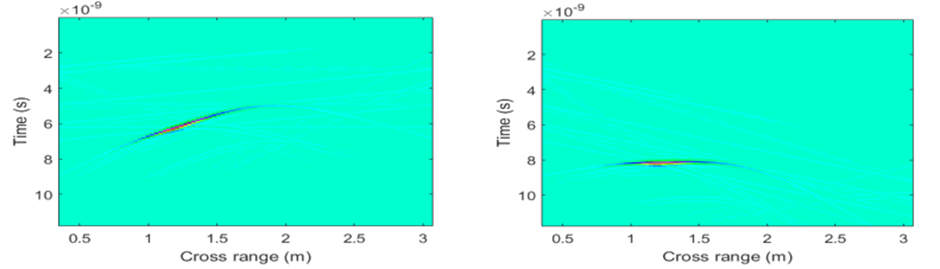
Fig. 20m. Left – After the SVD surface reflected wave removal; right – Final image
In order to test if the detection probability is increased by the integration of elevation correction and SVD surface reflected wave removal, the obtained B-scan is input into a Faster R-CNN network. The network isspecially trained for GPR systems and detection of objects with hyperbolic signatures in the B-scan. The simulated object is now a plastic cylindrical object with small diameter and relative dielectric permittivity ,purposely selected because of its low-reflective properties. Now the soil has relative dielectric permittivity . Notice the small difference between the reflected energies from the soil ( and from the object ( ). The performance of the neural network without and with surface wave removal is shown in Fig. 20n. The object cannot be detected if surface wave removal is not performed. However, when performing surface wave removal prior to detection, the object detection probability rises to 99%.
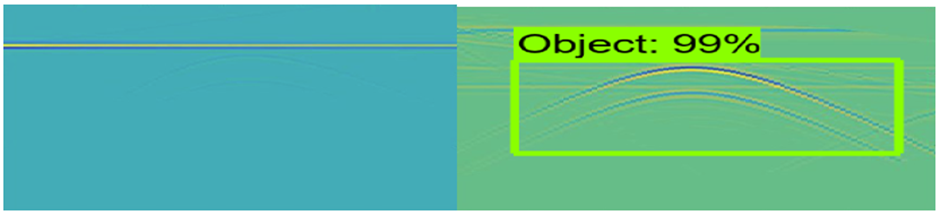
Fig. 20n. Left – Elevation correction only; right Elevation correction + Surface wave removal
To summarize, we proposed a post-processing method that integrates the elevation correction with SVD based surface reflected wave removal, to be used for UAV mounted GPR systems, operated above terrain with variable elevation. The aim is to increase the target detection probability, when dealing with low-reflective targets or targets masked by clutter. The method performance was tested and demonstrated using Faster R-CNN, pretrained for detection of hyperbolic signatures.
Part 4. Work done at UKIM on Land Mine Detection and Classification using Region Convolutional Neural Networks (R-CNN)
We now describe the automatic detection and classification of buried objects from GPR B-scans using Region Convolutional Neural Networks (R-CNN). We focus on the discrimination between anti-tank (AT) mines signatures and standard hyperbolic signatures obtained from other objects, including anti-personnel (AP) mines, using two classes in the R-CNN, the first called Object, and the second called AT-mine
Given the excellent results achieved by deep learning in many detection and classification tasks, we use the convolutional neural networks (CNN) using the TensorFlow open-source software library and Faster Region CNN (R-CNN) with Inception v2 configuration for COCO dataset. Convolutional neural networks have been used for detecting mines in previous work, but we focus on classification of the type of the mine. Anti-personnel (AP) mines give hyperbolic signatures that are similar with the signatures of many other objects (pipes, spherical objects, etc.). Therefore, we classify the objects with hyperbolic signatures as objects in the Object class. The AT mines give specific signatures, that are not hyperbolas. This fact enables to detect and classify two classes of objects, the first being AT mines, and the second being Objects with hyperbolic signatures. In a war zone, this effectively means discrimination between AT mines and AP mines. An image of interest can contain different objects that belong to different classes. We cannot know beforehand the number of objects in an image, and, therefore, this problem is not suitable for the application of standard convolutional networks. Objects of interest might have different spatial locations within the image and different aspect ratios. Faster R-CNN eliminates the standard selective search algorithm by adding a separate network (Region Proposal Network – RPN), used for prediction of the region proposals, object bounds and objectness scores at each position. Inception v2 network reduces computational complexity by factorizations of the convolutions into lower order convolutions. We train the network by using B-scan data generated by the gprMax software using models with different objects (AT mines, AP mines, other objects) and using corresponding data from the Web. The training and test data sets are shown in Table I, where the number of B-scans and the number of objects in the B-scans are shown.
| B – scans | ||
| Simulated B-scans (gprMax) | Real B-scans | Total |
| 48 | 109 | 157 |
| Objects presented in the B – scans | ||||
| Train data set | Test data set | Total | ||
| Hyperbolic objects | AT mines | Hyperbolic objects | AT mines | |
| 204 | 48 | 75 | 24 | 351 |
Table I. The training and test data sets
Figure 20o shows the results obtained using R-CNN, where object detection and localization with rectangular frames is shown. Also, the successful classification of an AT mine and two objects with hyperbolic signatures (in this case two AP mines) into the Object class is shown.
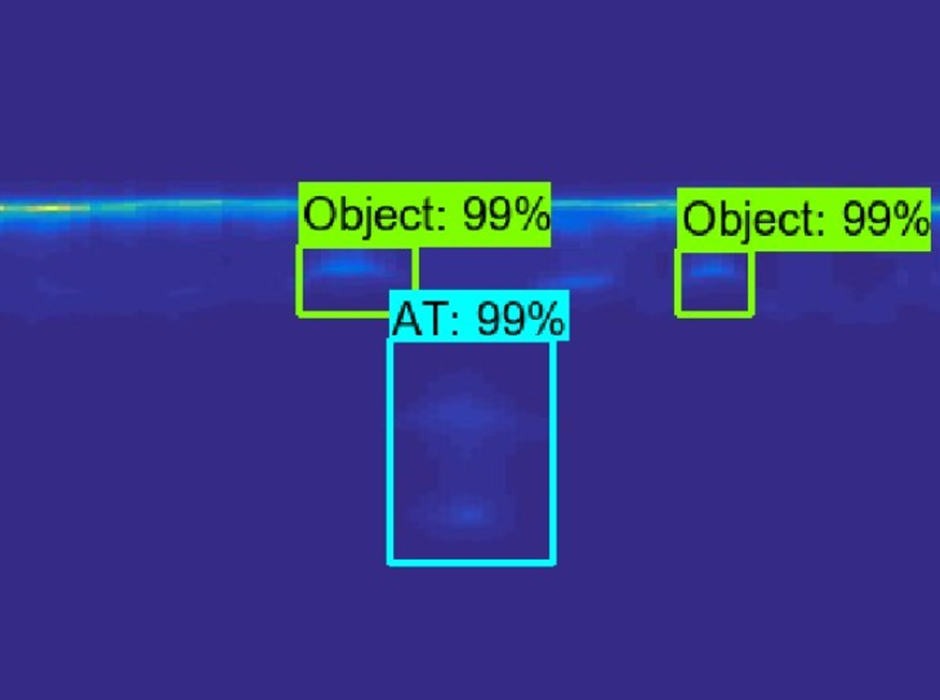
Fig. 20o. Object detection and classification with R-CNN
The second example shows object detection and classification, where three objects are classified in the Object class (i.e. neither of them is an AT mine). In fact, two of the objects are AP mines and the rightmost object is a metal can (Fig. 20p).
Fig. 20p. Object detection and classification with R-CNN
Additionally, we propose a post processing approach to discriminate between AP mines and other objects. The method is based on measuring the object size and its depth below the ground surface. AP mines are buried relatively shallow, approximately 1-2 cm under the soil surface. Their diameter is relatively small and can take values in the range 4-10 cm, newer models being smaller. This reduces the incorrect classification of the AT mines, which are buried deeper and are bigger than the AP mines. The main problem of this approach remains the use of non-standardized image representation and different image quality obtained from different GPR systems and the use of different image proportions and aspect ratios.
Publications published during the Project 3rd year period:
- Detection and Classification of Land Mines from Ground Penetrating Radar Data Using Faster R-CNN”, 26th Telecommunications Forum TELFOR 2018, Belgrade, Serbia.
- Paper in Explosives Detection, Sensors, Electronic Systems and Data Processing, Editors: Capineri, Lorenzo, Turmus, Eyup (Eds.), NATO Science for Peace and Security Series B: Physics and Biophysics.
- 14th International Conference on Advanced Technologies, Systems and Services in Telecommunications Telsiks 2019, Nish, Serbia.
- 14th International Conference on Advanced Technologies, Systems and Services in Telecommunications Telsiks 2019, Nish, Serbia.
Project presentations during the Project 3rd year period:
- ,Project presentation at the NATO SPS Security Conference held in Skopje, North Macedonia, 2-3July 2019.
- Project presentation at the IEEE IGARSS event in Maribor, Slovenia, 27 September 2019.
- Project presentation within the presentation of FEEIT and Signal Processing for Communications Laboratory at a CEEPUS project meeting held on 25 October 2019 during the Telsiks 2019 Conference in Nish, Serbia.
Ne New Equipment Purchased at UKIM during the Project 3rd year period:
- Vector Network Analyzer Keysight E5080B.
- Hexacopter DJI Matrice 600 Pro.
- Laptop HP EliteBook 1050.
- Tablet Samsung Tab A T290.
- Small Laboratory Power Supply.
- Uninterruptible Power Supply UPS Borri Galileo 2000 VA, 1800 W.
- Soldering Station Solomon SL-30.
- Raspberry Pi 4 microcomputer.
- Laboratory Small Tools (Pliers, Screwdrivers).
E Educational Achievements at UKIM during the Project 3rd year period:
- MSc student working on the project: Sinisha Pecov, mentor: prof. Venceslav Kafedziski.
- MSc student working on the project: Dimitar Tanevski, mentor: prof. Venceslav Kafedziski.
Researchers from BiH in the last period worked on establishing a connection with a drone using a microcontroller and stream coordinates to the target processor.
This part of project is about making correct path for DJI M600 with Google Earth coordinates.
We use STM32F4 microcontroller with DJI M600 and directly coding on it.
STM32f doesn’t have XML parser (library) which could be implemented into header, because of that we needed to change type from char coordinates to string.
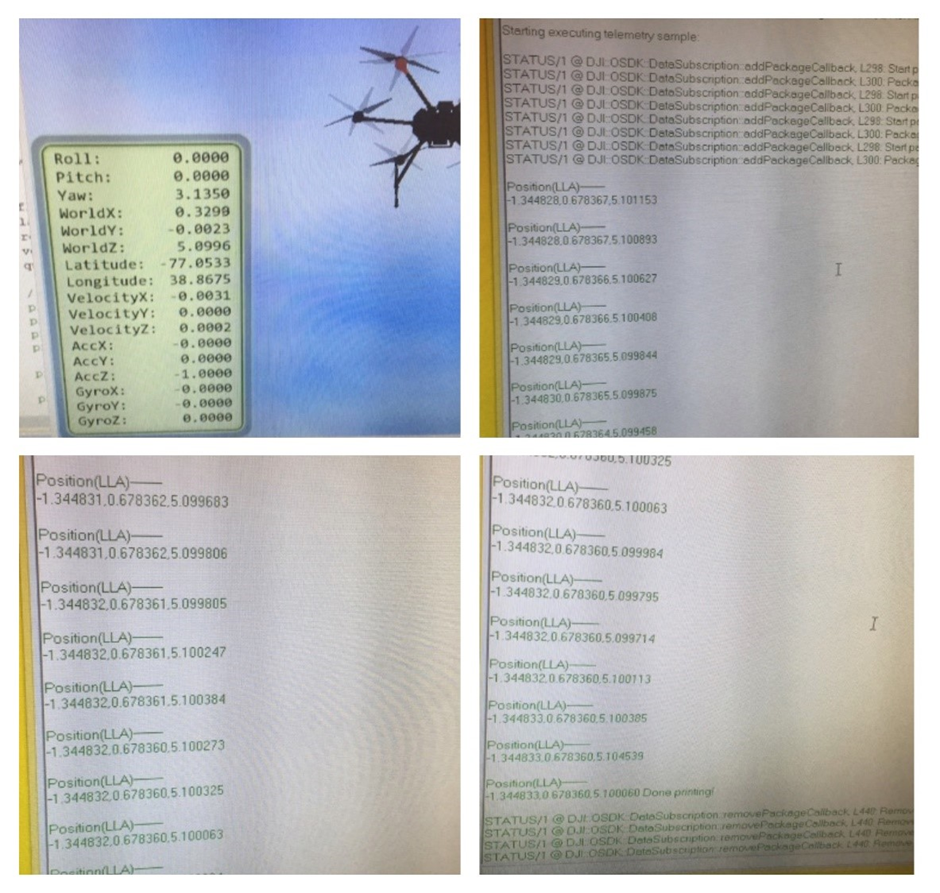
Fig. 21. Simulation of hexacopter flight path with corresponding location print-out.
Collaboration
The partnership between Macedonian, Bosnian and Slovenian universities has intensified in terms of knowledge transfer and enabling to perform real live experiments using developed hardware. All participating universities do not have regular funding for purchasing equipment, therefore this project provided the necessary infrastructure for radar implementation and enables knowledge transfer between researchers and institutions using good practices.
The project is multidisciplinary, including theoretical studies, hardware design aspects, software simulations, and signal processing and pattern recognition techniques. Therefore, exchange of knowledge and experience in all these fields among the partners is of crucial importance, especially when they have complementary expertise in some areas. Although the partners have sometimes developed their own approaches to some of the problems, depending on their own expertise, the exchange of the acquired experience during that process is of great benefit to all of them. The integration of all the developed approaches and techniques must be realized during the final year of the project to produce the final deliverables.
We organized several meetings in Maribor and Skopje, where we presented the work done over the last few months and discuss regarding issues, challenges and possible improvements.
Researchers at University of Maribor developed 2 different type of radars, stepped frequency radar and time domain radar. We have also made several ground experiments.
Researchers from Skopje designed software defined radar, compressed sensing radar and image processing for processing of radar data.
Researchers from BiH worked on drone localization and streaming GPS coordinated to the processing unit and integrate them into developed software.
The system for landmine detection consists of 4 major components: (a) hexacopter, which is called small Unmanned Aircraft System (sUAS)or drone, used for moving the radar platform over the landmines, (b) remote controller, which controls drone, (c) ground penetrating radar, which consists of microwave circuits for transmitting and receiving electromagnetic waves and (d) batteries, which represent the heaviest part of the system. The weight of the payload drastically influences the drone autonomy; therefore, the goal is to design a light weight and low-cost system for landmine detection. The data produced by the ground penetrating radar must be analysed to automatically detect landmines. This research is focused on developing new methods for landmine detection using new hardware and software solutions.
The specific deliverables of the project are:
- Ground penetrating radar attached to a hexacopter
- Software for landmine detection, localization and classification
The scientific approaches to development of ground penetrating radar are:
- Development of a stepped frequency radar
- Development of an impulse (UWB) radar
- Development of a random frequency stepped frequency radar with compressive sampling
The scientific approaches to landmine detection, localization and classification are
- Hyperbola detection with its vertex determination
- Machine learning and artificial intelligence approaches for detection and classification
Training & Professional Development
The following young researchers were involved in the project, who are currently working on their PhD and MSc degrees.
- Danijel Šipoš, Slovenia, PhD Student
- Blaž Pongrac, Slovenia, PhD Student
- SinišaPecov, Macedonia, MSc Student
- DimitarTanevski, Macedonia, Diploma graduate
- Alen Helać, BiH, Msc Student
- DženitaVejsilović, BiH, Msc Student
- Lejla Selimović, BiH, MsC., student
Impact
This project demonstrated the use of advanced concepts for landmine detection. The deliverables enabled to assemble small radars and attach them to commercially available drone platforms. The time needed for landmine detection is be reduced, because the drone platform is be able to automatically scan the area within 20 minutes using velocities of up to 15 km per hour.
The proposed method of land mine detection using a drone mounted GPR is ecologically clean, non-hazardous, non-destructive, technologically advanced, efficient and fast. GPR is a type of radar that can find numerous applications in different sectors, such as utility location, structural assessment, archaeological survey, environmental applications, geotechnical applications, law enforcement, grave location and cemetery mapping. Developing a simple and efficient GPR with advanced signal processing and pattern recognition techniques could have an impact on all these areas. Some researchers have used the GPR to develop GPR based techniques for vehicle localization and autonomous driving, using pre-recorded underground maps obtained by GPR measurements, that use stable subsurface features. More generally, developing a lightweight radar that can fly on a drone can potentially find many other applications besides its use for detection of underground objects, such as for land remote sensing.
The results pertaining to the radar solution and its hardware development and implementation, developed by the partners are be publicly available, and the potential end-users are be able to build a similar device. We also provide consulting for hardware development, which enables sustainable use of results.
Security Relevance
The topic of the proposal is linked to the “Mine and UXO Detection and Clearance” objective is the SPS Key Priorities. The development of radar-based device for automatic landmine detection addresses directly the SPS Key Priorities. The development of such radar has the following improvements:
• The objective is to make land mine detection faster, easier and more efficient. Current systems can move with velocity of 3km/h. The goal is to develop a platform, which can move at a velocity above 15km/h and cover 3m of area in range direction
• The use of compressed sensing within the process of radar techniques enables faster data acquisition
• The automatic landmine detection is an objective of this proposal. The development of land mine detection using acquired radar data is based on analysing the radar profiles. These profiles can be analysed after the electromagnetic waves reflected off the object, buried under the surface, arrive at the receive antenna. Since the goal is to develop fast detection, in the process of reconstruction compressed sensing techniques can be used to achieve faster reconstructions using only few samples.
Mine detection is of enormous relevance to protect people and prevent any contacts with landmines to prevent injuries. Although numerous techniques for mine detection exist, each of them suffers from some disadvantage. Some of them, such as manual detection pose danger to the human operator. Recently, armoured demining vehicles, that are remotely controlled, have been used for both detection and demining. However, using a drone mounted GPR has advantages over all the other techniques of land mine detection, since it avoids inflicting casualties and/or damage to the vehicle that moves on the ground surface. Also, it enables access to rough terrains, and terrains covered with vegetation. Mine classification that we also address in this project is also very important, since knowing the type of mine buried in the ground could provide information for choosing a suitable method of demining. Using modern methods of machine learning, such as Deep Convolutional Neural Networks could facilitate land mine detection and classification. The achievements of this project could be used in other areas, which require the use of drones, radar design knowledge, and knowledge of machine learning techniques for classification.
Advances of the “science pillar” of NATO SPS
The proposed project is hardware and software oriented. The hardware is developed using standard components. It is known that the GPR hardware is very expensive, therefore our goal is to propose a low-cost solution and make the principles of the solution available on a web site, such that the end users can reproduce the experiments.
Besides the hardware development, some new methods for real time landmine detection were investigated. Compressed sensing methods, which can recover the original signal using fewer samples than the theoretical bound are intensively researched. These methods enabled landmine detection using real time acquisitions.
The project proposes a device, which works in 2 modes. The first mode is a classical GPR technique, which is widely used in GPR. The second one, compressed sensing stepped frequency radar is a novel technique, which uses a set of different random frequencies. The advantage of this method over the other is that it is able to detect objects using a multi-frequency approach, which differently characterizes targets and helps to make the detection of buried objects more reliable.
The Synthetic aperture radar technique is a radar-based technique, which uses a moving platform to simulate synthetic aperture. This technique produces three dimensional approaches to monitoring subsurface targets. The advantage of this technique is to monitor not just a single point in subsurface, but to monitor wider area. The goal of the project is to capture 3m wide area using a flying device, the hexacopter, which are able to move at a constant velocity. The Synthetic Aperture Radar techniques improve landmine and objects visibility within radargram.
The second part of the project aims at the automatic detection of buried mines. Land mine detection techniques based on radar data analysis were developed using our proposed radar implementations, where buried objects are detected using hyperbola detection or pattern recognition tools, such as Deep Convolutional Neural Networks (CNN). Hyperbola detection can be done using the Hough transform, after a suitable pre-processing of the obtained images from the GPR. Deep CNN offer additional possibilities to do object classification, i.e. to distinguish between landmines and other objects, or to distinguish between anti-personnel and anti-tank mines, or as a goal, to classify different types of mines in different classes. Classifying the detected land mines would enable to undertake an appropriate and convenient demining approach.
As can be seen, this project includes many hardware and software-oriented activities, using the most advanced modern scientific achievements, such as advanced hardware implementation techniques, compressive sampling, advanced methods of image processing, and advanced classification techniques using the most recent implementations of deep neural networks.
Implementation
Figure 8 shows an implementation of the Stepped frequency radar on a single PCB board. The radar is lightweight and small in dimensions, 120mm×50mm, and weights 300g with all connectors and elements. Figure 22 shows implementation of time domain radar with antenna integration. This form was suitable for attachment to the hexacopter.

Fig. 22. Implementation of time based GPR
Figure 23 shows implementation of Steeped frequency radar attached to the hexacopter. In Fig 23. Receiving and transmitting antennas are depicted and batteries are depicted. The total weight of the payload with batteries and antennas was 2kg. In Figure 24 a radargram obtained with the steep frequency radar is depicted, with a clear evidence of a possible landmine detected. Figures 24-26 show landmine detection using stepped frequency radar. We have test it on a test site Benkovac, custom landmine field and test site in Macedonia. Buried object are marked in Figs. 24-26 and typical hyperbolas can be noticed. Figure 27 show the radargram obtained with the time domain radar at a Benkovac test site.

Fig. 23. Radars attached to the hexacopter. left) Stepped Frequency Radar. (right) Time domain-based radar
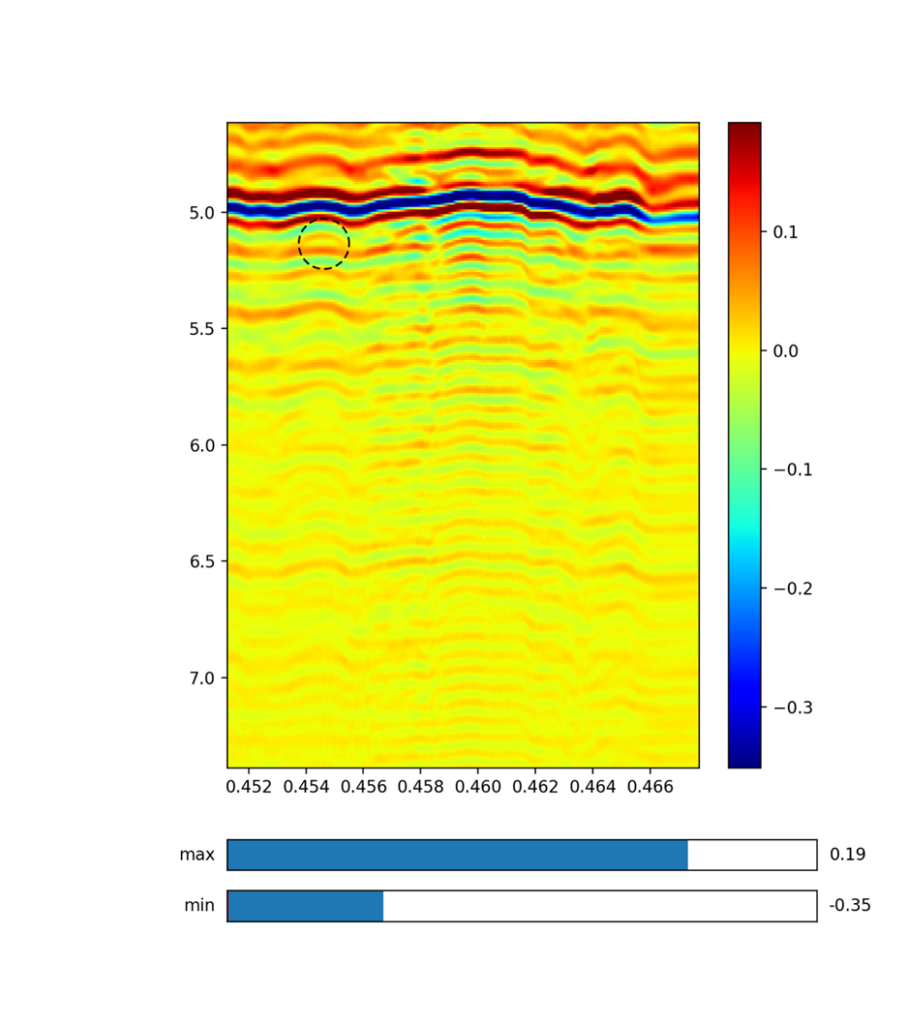
Fig. 24. Radargram obtained in Benkovac using Stepped frequency radar, where the presence of landmine is pointed with dashed lines.
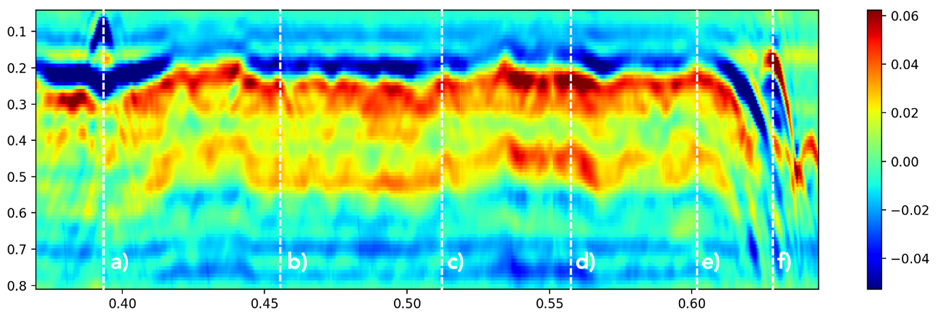
Fig. 25. Radargram obtained using Stepped frequency radar at custom made landmine polygon, where line a) and f) indicates reference corner reflector and b) to f) buried landmines.
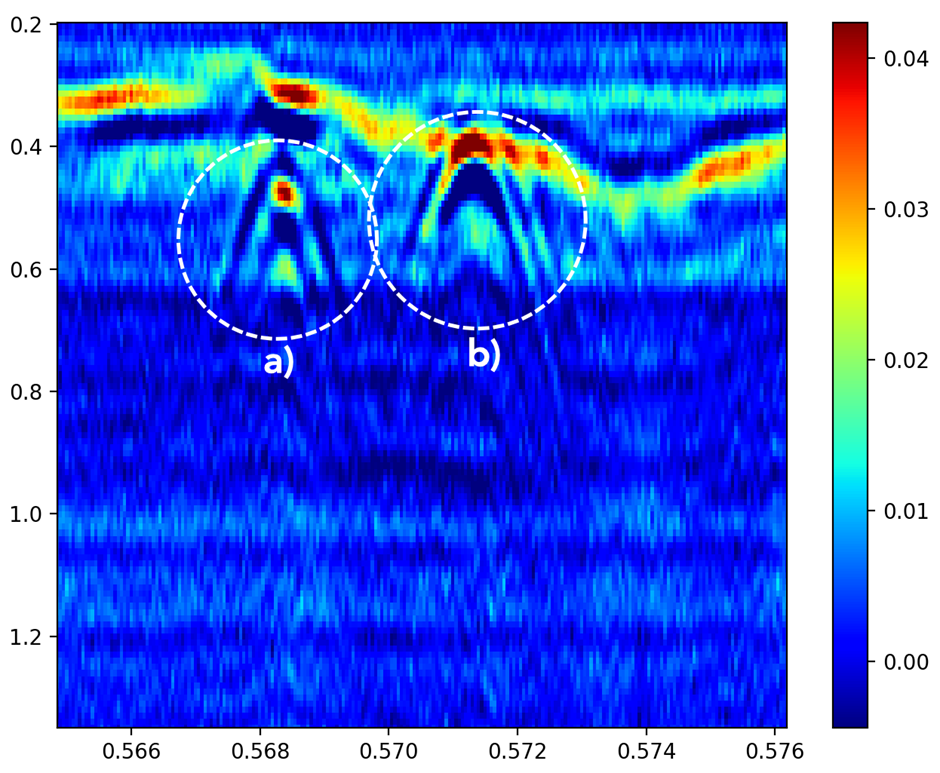
Fig. 26. Radargram obtained using Steeped frequency radar in Macedonia. Where a) shows buried AT landmine and b) reference corner reflector
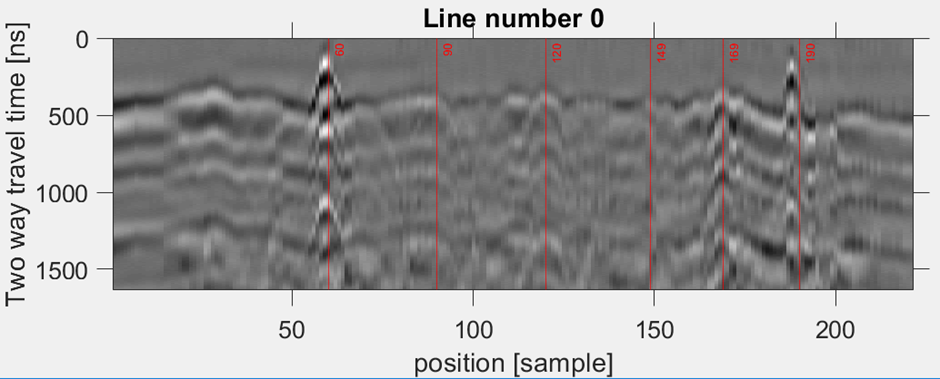
Fig. 27. Radargram obtained using Time domain radar at custom made landmine polygon (left and right red line indicates corner reflectors, lines in middle indicates four buried mines).
Measurements were performed in Benkovac region, on 6th of May 2019, in Slovenia at custom based landmine field on 1st of October 2019 and in Macedonia on 29th of October 2019. Configuration of ground vehicle and hexacopters are depicted in Figure 28. In Benkovac test site it was very windy (strong Bora wind) at the time of acquisition, therefore it was impossible to fly with a hexacopter, therefore we improvise with a ground vehicle.

Fig. 28. (Top left, right middle left). Images from test site Benkovac with an improvised vehicle due to strong Bora wind. (middle right) Stepped frequency radar attached to a hexacopter on a test site in Macedonia. (bottom left and right) Time based radar attached to a hexacopter in Slovenia.
Power consumption of Pulse Radar
Both radars had implemented power supply using Li-Po 6S battery with 5 Ah capacity. Radar uses two power modes. In normal mode only processor board with attached WiFi and GPS modules is connected to power supply. Power consumption in normal mode is around 10 W. The biggest consumer is RF amplifier with consumption of 12 W. Due to big consumption we implemented scanning mode when we manually turn ON RF amplifier using GUI. In scanning mode, the autonomy of radar is around 3 hours and in normal mode about 6 hours, respectively.
Controlling pulse radar
For controlling pulse radar, we implemented GUI using Matlab. GUI can be used on laptop or PC with installed Matlab (platform independent). GUI also support real-time data transfer and graphical representation. Communication is established via ethernet or WiFi. Using GUI, we can control Start and Stop of scanning mode, we can set IP address, offset of received signal and number of averaged samples. Also, we can save received data. Additional option is to manually set markers to indicate objects.
Radar monitoring
All parameters and received data are represented using same GUI as for control the radar. GUI showing each received signal on left side and Radargram in the middle. On the right-side showing GPS coordinates, velocity of drone, number of scanned samples, time of scanning. See figure below.
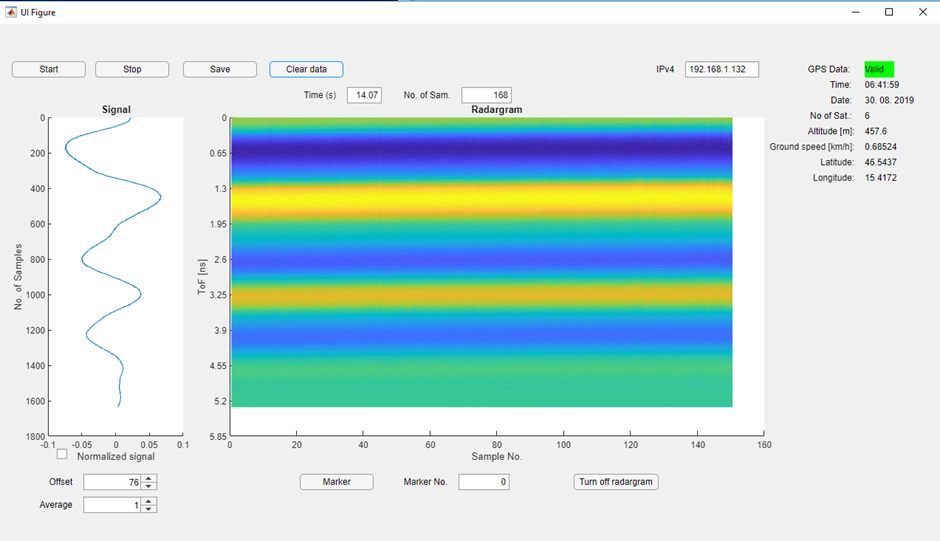
Fig. 29. GUI for pulse based GPR radar system
Batteries of SFCW radar
The single board developed SFCW Radar uses an external 3S Li-Po battery with 1300 mAh capacity. Since the power consumption in transmit – receive mode is only about 350 mA at 12 V, with the chosen battery a working time of at least 3 hours is guaranteed and doesn’t limit the drone flight time. External battery pack was used to isolate noise which could be caused from drone components as motors and motor drivers. The SFCW radar power consumption therefore doesn’t limit the drone autonomy, but only the radar weight itself. With total payload of 2.5 kg the total drone autonomy is about 20 minutes and is also highly influenced by the wind strength.
Controlling SFCW radar
The SFCW radar takes the advantage of drone open-source Software Development Kit (SDK) and is capable to be triggered from the remote controller (RC) over a custom defined button. For avoiding additional equipment, the measurements are stored to a SD card which is directly plugged to the radar board. Since wind can cause flight path disturbances also real-time geo-location is stored to the SD card and simplifies the post-processing process. For test procedures with additional RC button also possible landmine location can be stored at given point.
Monitoring of SFCW radar
Since the data is captured locally to a SD card, post-processing is needed to obtain a radargram. A custom program was developed in Python language which includes basic radar processing tools for easier analysis with capability of use on different-operating system platform. The Graphic User Interface (GUI) is shown on image below.
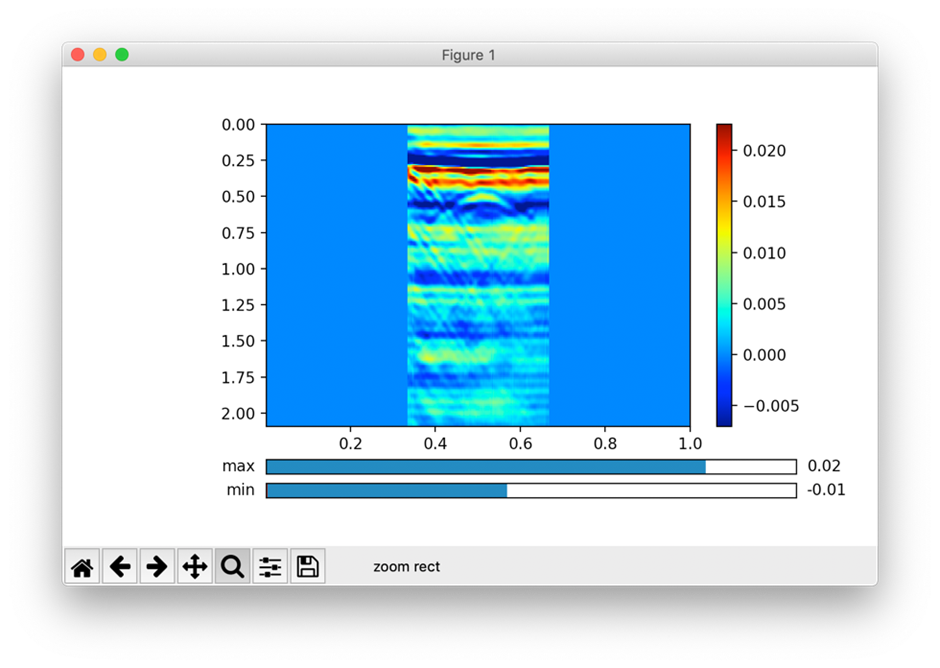
Fig. 30 GUI for SFCW radar system.
Project Participants and Roles
| Name | Affiliation | Position/Title | % Time | Role |
| Prof. dr. Dušan Gleich | University of Maribor, Faculty of Electrical Engineering and Computer Science (UM-FERI) | Prof. Dr. | 20% | Management, project leader, radar development, testing and publishing results |
| Danijel Šipoš | UM-FERI | Young researcher | 30% | Radar design and development, testing, hardware platform |
| Peter Planinšič | UM-FERI | Assoc. prof. | 5%% | Communications, Dissemination of project results |
| Andrej Sarjaš | UM-FERI | Assist. Prof. | 5% | RF measurement design, hardware platform design and testing |
| Marko Malajner | UMFERI | assistant | 10% | Antenna design, time domain radar, publications |
| Venceslav Kafedziski | Ss Cyril and Methodius University in Skopje, Faculty of Electrical Engineering and Information Technologies (FEIT) | Prof. Dr | 25% | USRP Prototyping, Continuous Wave Stepped Frequency Radar, GPR processing |
| Sinisha Pecov | FEIT | Young Researcher | 15% | USRP Prototyping, Continuous Wave Stepped Frequency Radar |
| Dimitar Tanevski | FEIT | Young Researcher | 15% | USRP Prototyping, Continuous Wave Stepped Frequency Radar |
| Emir Skejić | University of Tuzla, Faculty of Electrical Engineering (UT) | Associate professor | 5% | Testing Equipment |
| Amira Šerifović-Trbalić | UT | Assitant prof. | 5% | Pattern Recognition |
| Alen Helać, Đenita Vejsilovič, Lejla selimović | UT | Young researcher | 15% | Hexacopter utilization |
Criteria for Success
| Criterion | Relative Weight | Complete | Comments |
| USRP prototyping | 5% | 100% | We made a study for GPR and hexacopter design. |
| Antenna design | 5% | 100% | We have chosen an antenna design, that gave the best frequency response for our needs. It is the second most important part of the radar. |
| Hardware platform | 50% | 100% | We designed our hardware platform, based on FPGA. |
| Continuous wave radar | 10% | 100% | We designed our hardware platform, based on FPGA. |
| Sparse Random Frequency Radar | 5% | 100% | We designed stepped frequency radar with the USRP. |
| Principles of SAR GPR and focusing | 10% | 100% | We designed SAR GPR. It is suitable for a stable regions. |
| Testing with end-users | 5% | 70% | We made tests with some of end users. This task is still open, because many users are interested in hardware. |
| Dissemination | 10% | 90% | We published several conference papers, journal papers are coming soon. |
| In depended testing of 5 devices | 1% | 100% | We made 3 operational devices. |
Products & Dissemination
Journal articles, conference papers, book chapters, and other publications (please do not attach copies)
V. Kafedziski, S. Pecov, “Implementation of a High Resolution Stepped Frequency Radar on a USRP”, Proceedings of 13th International Conference on Advanced Technologies, Systems and Services in Telecommunications TELSIKS 2017, Nish, pp. 236-239.
V. Kafedziski, “Implementation of a Compressive Sampling Stepped Frequency Radar on a USRP”, Proceedings of 14th Conference ETAI 2018, Struga.
V. Kafedziski, S. Pecov, D. Tanevski, “Target detection in SFCW ground penetrating radar with C3 algorithm and Hough transform based on gprMax simulation and experimental data”, Proceedings of 25th International Conference on Systems, Signals and Image Processing IWSSIP 2018, Maribor.
V. Kafedziski, S. Pecov, D. Tanevski, “Detection and Classification of Land Mines from Ground Penetrating Radar Data Using Faster R-CNN”, Proceedings of 26th Telecommunications Forum TELFOR 2018, Belgrade.
V. Kafedziski, Project presentation at the Workshop organized for the NATO SPS SIARS Project, 24 October 2017, held at the Military Academy in Skopje, with the presence of high NATO representatives and Minister of Defenseof Republic of Macedonia.
V. Kafedziski, Project presentation including an exhibition of the USRP hardware and project brochure dissemination at the first Western Balkans Digital Summit, Skopje, 18-19th April 2018.
D. Gleich, V. Kafedziski, Ground Penetrating Radar Attached to a Hexacopter for Automatic Mine Detection, Project presentation at the NATO SPS Advanced Research Workshop on Explosives Detection, Florence, 17-18th October 2018.
D. Šipoš, D. Gleich, Blaž Pongrac, Developing of stepped frequency radar for landmine detection, IWSSIP 2018
D. Šipoš, D. Gleich, Blaž Pongrac, Deep neural networks for classification of SAR data, IGARSS 2018
D. Šipoš, D. Gleich, Deep neural networks for despeckling of SAR data, IGARSS 2019.
Dušan Gleich, Peter Planinšič, SAR patch categorization using Dual tree oriented wavelet transform and Stacked Autoencoder, on conference IWSSIP 2017 http://iwssip2017.org/
Dušan Gleich, Peter Planinšič, Danijel Šipoš, Deep Convolutional Neural Networks for SAR Patch Categorization, presented at Elmar 2017, Zadar, Croatia.
Blaž Pongrac, Deep Convolutional Networks for SAR data categorization, Presented at ERK 2017, Portorož, Slovenia.
Peter Planinšič, Dušan Gleich, InSAR Patch Categorization using sparse coding, IEEE Geoscience and remote sensing Letters, June 2017.
Conference presentations and public lectures
V. Kafedziski, S. Pecov, “Implementation of a High Resolution Stepped Frequency Radar on a USRP”, Proceedings of 13th International Conference on Advanced Technologies, Systems and Services in Telecommunications TELSIKS 2017, Nish, pp. 236-239.
V. Kafedziski, “Implementation of a Compressive Sampling Stepped Frequency Radar on a USRP”, Proceedings of 14th Conference ETAI 2018, Struga.
V. Kafedziski, S. Pecov, D. Tanevski, “Target detection in SFCW ground penetrating radar with C3 algorithm and Hough transform based on gprMax simulation and experimental data”, Proceedings of 25th International Conference on Systems, Signals and Image Processing IWSSIP 2018, Maribor.
V. Kafedziski, S. Pecov, D. Tanevski, “Detection and Classification of Land Mines from Ground Penetrating Radar Data Using Faster R-CNN”, Proceedings of 26th Telecommunications Forum TELFOR 2018, Belgrade.
V. Kafedziski, Project presentation at the Workshop organized for the NATO SPS SIARS Project, 24 October 2017, held at the Military Academy in Skopje, with the presence of high NATO representatives and Minister of Defense of Republic of Macedonia.
V. Kafedziski, Project presentation including an exhibition of the USRP hardware and project brochure dissemination at the first Western Balkans Digital Summit, Skopje, 18-19th April 2018.
D. Gleich, V. Kafedziski, Ground Penetrating Radar Attached to a Hexacopter for Automatic Mine Detection, Project presentation at the NATO SPS Advanced Research Workshop on Explosives Detection, Florence, 17-18th October 2018.
D. Šipoš, D. Gleich, Blaž Pongrac, Developing of stepped frequency radar for landmine detection, IWSSIP 2018
D. Šipoš, D. Gleich, Blaž Pongrac, Deep neural networks for classification of SAR data, IGARSS 2018
D. Šipoš, D. Gleich, Blaž Pongrac, Landmine detection using steeped frequency radar, IWSSIP 2019
D. Šipoš, D. Gleich, Deep neural network for despeckling of SAR images, IWSSIP 2019.
Dušan Gleich, Peter Planinšič, SAR patch categorization using Dual tree-oriented wavelet transform and Stacked Autoencoder, on conference IWSSIP 2017 http://iwssip2017.org/
Dušan Gleich, Peter Planinšič, Danijel Šipoš, Deep Convolutional Neural Networks for SAR Patch Categorization, presented at Elmar 2017, Zadar, Croatia.
Inventions, Patents, & Licenses
Other products such as web sites, databases, etc. released to the scientific community or the public au.feri.um.si/losdv/en/gpr_projekt/
Project publicity (please attach copies of articles or reports about the project)
We were actively invloved in organizing conference IWSSIP 2018, where the results were presented.
We presented our activities at IGARSS 2018, IGARSS 2019 and Elmar 20118.
Within the Bilateral project with University of Fuzhou, China we presented activities of the project.
We presented project at CEEPUS meeting in Sofila, Bulgaria 2019
The project was presented in Niš, Serbia at Telkis Conference, October 2019.
The project was presented in Slano, Croatia 2019 at Landmine conference.
The project was presented in Tokyo, Japan 2019 at IGARSS 2019.
The project was presented in Graz, Austria 2019 at TelCon 2019.
The project was presented in Rome, Italy 2019 at PIERS 2019.
The project was presented in Skopje, Macedonia in October 2019.
We organized Slovenian IEEE Remote Sensing Chapter.
